Основы математического аппарата и математические модели линейных ДСАУ. Решетчатые функции, страница 3

НТР породила интенсивную разработку новых разделов  теоретической физики. В ЛПИ, например, кроме "физмеха" создается еще РФФ (1952 г.), а затем ещё и "физтех"(1988 г.). Поразительные "сдвиги "произошли и в "консервативной математике". За (20 - 30) лет формируется новая прикладная математика  с целым рядом разделов, которую принято именовать " Дискретной математикой" (ДМ) (синоним Дискретный анализ). Вот краткое пояснение этого понятия (на основе "Математический энциклопедический словарь" // Глав. Ред. Ю.В.Прохоров . Изд. - во "Советская Энциклопедия. - М.: 1988.).

Дискретная математика занимается изучением свойств моделей  дискретных структур, которые возникают как в самой математики, так и в её приложениях, таких как, модели различных систем обработки и преобразования информации.

В отличие от ДМ, классическая.математика занимается изучением свойств моделей  объектов непрерывного характера.

Разделы ДМ в приложениях разнообразны и их количество продолжает расти. К ним относятся: вычислительная математика ,теория конечных автоматов, математические основы теории управления ( например, в работе [3] "математическим основам управления импульсными системами" отведено более 300 страниц текста из 950), математические методы анализа алгоритмов, математическая логика и др.

Не следует думать, что все эти разделы ДМ возникли "вдруг". Просто они вобрали в себя многие знания, накопленные столетиями и, даже, тысячилетиями, трансформированые для конкретных приложений. Взять, хотя бы, математическую логику! Исчисление высказываний ("да", "нет" - "истинно", "ложно") многие века считались понятиями философии. Даже разработка "алгебры логики" (алгебры состояний) Джорджем . Булем (1815 - 1864) мало что изменил. Но в XX веке потребовалась теория анализа, синтеза и оптимизации сначала  контактных релейных, затем бесконтактных электронных систем автоматики и ,далее, систем на базе промышленных контроллеров. Отвечая насущным нуждам практики, и сформировалась современная математическая логика. Конечно, в логике работают и "чистые" математики, труды которых нам, сугубым "прикладникам," понять трудно, поскольку мы говорим "на разных языках".

Итак, Родион , все что Вы перечислили относится к Дискретной математике, которая имеет широкий спектр разделов. Первые два помянутыхВами труда, видимо, предназначены теоретикам - математикам, а курс лекций уважаемого Виктора Александровича предназначен и полезен нам с Вами.

Разности высших порядков определяются рекуррентными соотношениями (другое название "возвратные соотношения") – т.е. через разности предыдущих порядков. Например, разности 2-го порядка:

Δ²f[n,ε]=Δf[(n+1),ε]–Δf[n,ε] – прямая неразделённая;

Δ²f[nT,ε]=(Δf[(n+1)T,ε]–Δf[nT,ε])/Т – прямая разделённая;

Ѳf[n,ε]=Ñf[n,ε]–Ñf[n–1,ε] – обратная неразделённая;

Ѳf[nT,ε]=(Ñf[nT,ε]–Ñf[(n–1)T,ε])/Т – обратная разделённая.

И вообще для разностей любого порядка:

Δ^k+1f[n,ε]=Δk f^.[n+1,ε]– Δ^k f [n,ε] – прямая неразделённая;

Δ^k+1f[nT,ε]= (Δk f^.[(n+1)T,ε]–Δk f^.[nT,ε])/Т – прямая разделённая;

Ñ^k+1f[n,ε]=Ñ^k f[n,ε]–Ñ^k f[n–1,ε] – обратная неразделённая;

Ñ^k+1f[nT,ε]=(Ñ^k f[nT,ε]–Ñ^k f[(n–1)T,ε])/Т – обратная разделённая.

Подставляя в эти формулы аналогичные же формулы для разностей все более низких порядков, можно перейти к представлению разностей k-го порядка через k+1 значений исходной функции. Например:

Δ²f[n,ε]=Δf[(n+1),ε]–Δf[n,ε]=f[(n+2),ε]–2f[(n+1),ε]+f[n,T]

Ѳf[nT,ε]=(Ñf[nT,ε]–Ñf[(n–1)T,ε])/Т=(f[nT,ε]–2f[(n–1)T,ε]+f[(n–2)T,ε].

Вообще коэффициенты, с которыми входят в это выражение значения исходной функции определяются из комбинаторных соображений и записываются через число сочетаний. Таким образом, общая формула, например, для обратных разделённых разностей k-го порядка следующая:

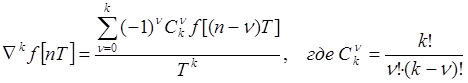.                                      (11.1.)

Для неразделённых прямых и обратных разностейk-го порядка получим: