Основные материалы по использованию критерия Гарри Найквиста. Методика получения асимптотических псевдочастотных характеристик для дискретных систем разной структуры, страница 2

"Упругости второго рода" связаны со свойствами обрабатываемых материалов в сложных технологических установках ( упругости бумажного полотна (картона) в сушильной части бумагоделательных машин, в системах" раскат" - "накат" бумагорезательных машин, в листовых и "фасонных" прокатных станах, в "моталках" проволоки и др. агрегатах металлургической промышленности. Все "упругие  звенья" в ЭМС появляются при повышении интенсивности рабочего процесса. В математической модели ЭМС "электропривод подачи" металлорежущего станка упругое звено имеет параметры высокочастотного колебательного звена. Характеристики таких звеньев представлены в файле Табл.14.а doc строками "14" и "15". Модель ДСАУ в этом  случае представлена как ИС с экстраполятором Э₀.

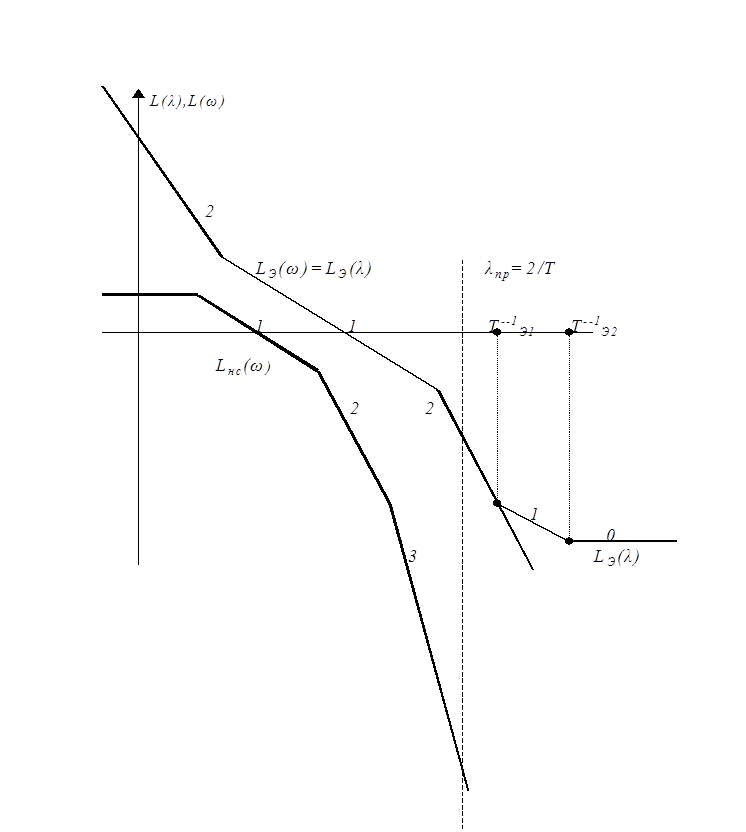Рис. 5. 12

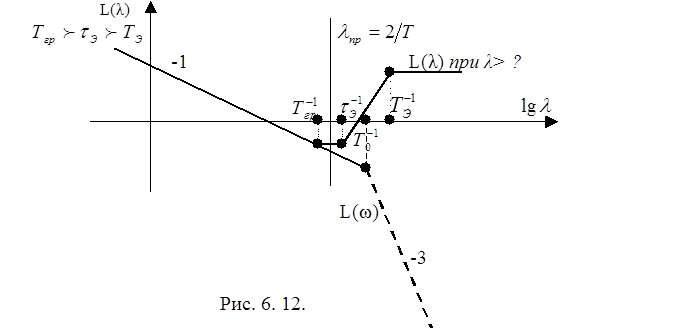
Пример. Исследуем модель ИС, соответствующую строке "14". Её параметры находим в "Пояснении 1. На рис 6. 12 изображена высокочастотная часть л. а. х. ИС, которая показывает, что при таком транспонировании высокчастотных параметров система будет неустойчивой. При другом соотношении параметров Т_гр и τ_Э характерстика L(λ) существенно не изменяется ( см. рис. 7.12).

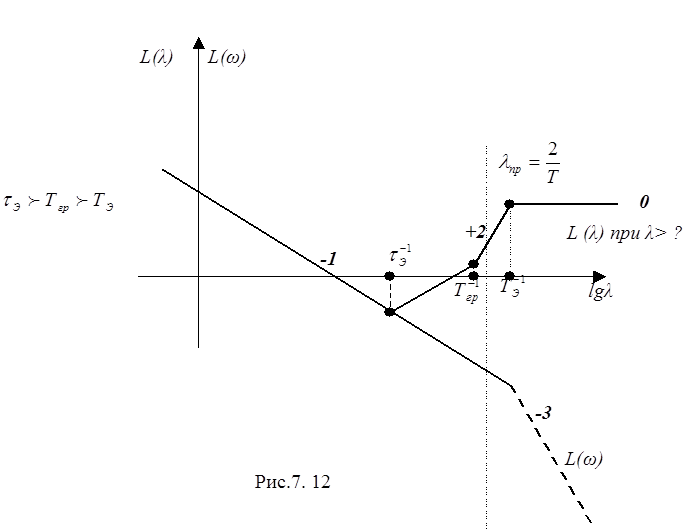
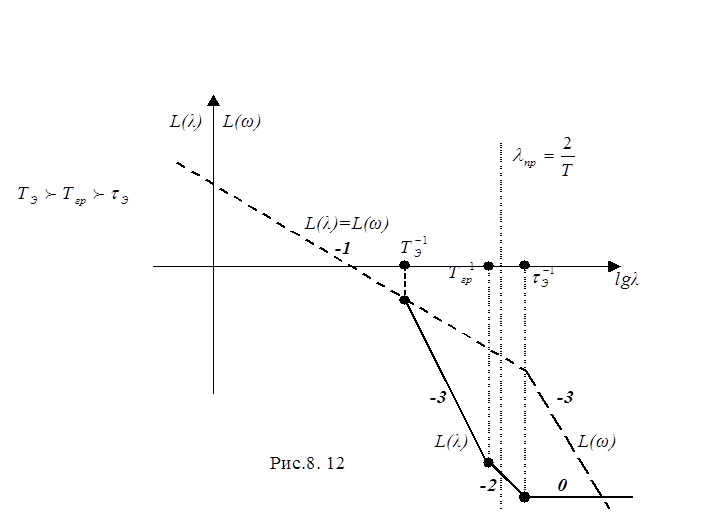
Только при соотношении T_Э>τ_Э достигается устойчивость импульсных систем с высокочастотными упругими звеньями (см. рис 8. 12).

Такие же явления происходят и в ДСАУ с упругим звеном, если высокочастотная часть L(ω) имеет вид (-2) - (-4) (рис.9. 12). Параметры этой модели представлены в строке"15" файла Табл.14.а doc, и там же в "Пояснении 2".

Для импульсных систем с экстраполятором первого порядка характеристики K(w,0) представлены строками "4" - "8". При реализации эквивалентных экстраполяторов используют характеристики из строк "9" - "11". Далее следует выбрать, в зависимости от конкретных значений параметров синтезируемой ДСАУ, один из тех же пяти вариантов синтеза. Напомним, что область, где L(ω) ≈ L(λ), сужается до λ_пр=(Т)^-1.

9. 3. Разновидности синтеза регуляторов в цифро - аналоговых систем (ЦАС)

Здесь мы применяем способ задания эталонной асимптотической л. а. х. ДСАУ L_Э(λ).  Это обусловили следующим.

Во - первых, приняли невысокие порядки базовых моделей регулятора и объекта.

Во - вторых, базовым считаем ПИ регулятор.

В третьих, "прототипом " для ЦАС считаем аналоговую САУ с L_Э(ω)вида

-.2- 1 - 2 или -2 -1 -2 -3.

Эти условия обоснованы следующими причинами.

1. Модели реальных ЭМС имеют (3 - 5) порядок, точнее на динамику такой модели САУ влияют (3 - 5) доминирующих корня.

2. Пропорционально - интегральный (ПИ) регулятор наиболее часто используется на практике. В дальнейшем рассмотрим синтез ЦАС и с ПИД регуляторами.

3. Эталонная структура -.2 -1 - 2 обеспечивает нулевые ошибки по полжению и скорости при любых значениях добротности по ускорнию (к_а ).

Тогда ДПФ эталонной структуры (рис. 3. 12) будет такой.

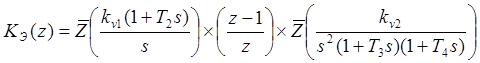,                            (2.12)

где

При вариациях β выражение (2. 12) позволяет получить различные характеристики L_Э(λ). Так, при γ=0 имеем L_Э(λ) вида: 2 - 1 - 2 - 1 - 0, а при ,

соответственно, 2 - 1 - 2 - 3 - 2 - 1 - 0.

Показатели качества ЦАС представлены в Табл. 2. Характеристики по формуле (3. 12) были рассчитаны в лекции 9 и вПриложении 9 к той же лекции .

В расчетах задаются значениями Т, Т₃ и σ_макс , вычисляют и находят в Табл. 2 значение М удовлетворяющее этим условиям. Далее вычисляют , . и

В литературе по теории дискретных систем рассматриваются принципы построения только ЦАС. Реально же большинство электромеханических систем – это АЦАС. Следовательно, надо уметь синтезировать оба вида структур. Последняя задача рассмотрена ниже.

Из всех методов синтеза наиболее разработан для инженерных применений структурно - параметрический метод Динамического Синтеза (ДС) В А. Бесекерского.