Построение выборочной функции распределения. Гистограмма. Точечные оценки моментов

Расчётное задание №2

Работу выполнил студент     2081/1                 

группа                               ФИО

Преподаватель                              

подпись                              ФИО

Вариант 12

Часть 1

В результате измерений получена выборка   из генеральной совокупности с неизвестным законом распределения

1.  Построить :

1.1  Выборочную функцию распределения F(x)

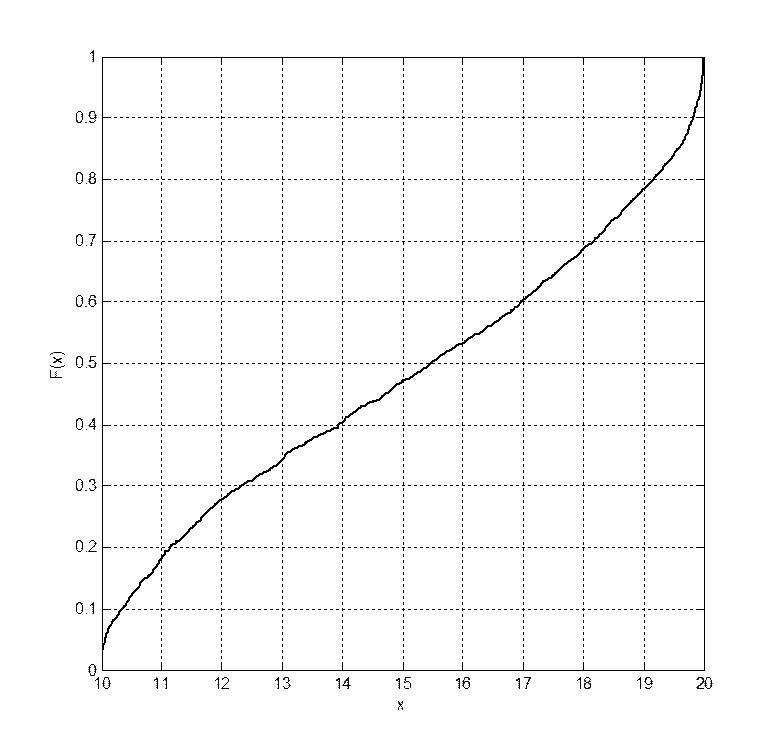
Рис.1 Выборочная функция распределения F(x)

1.2  Гистограмму

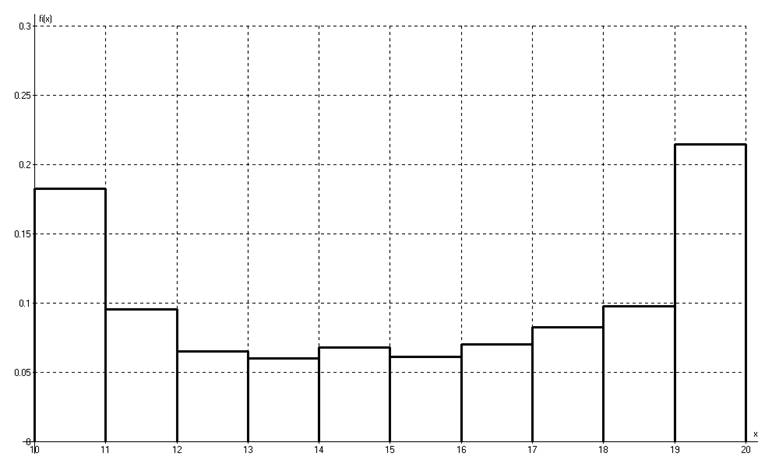
Рис. 2 Гистограмма

2.  Вычислить :

2.1  Точечные оценки :

2.1.1  Моментов

Для  оценки моментов использовались следующие формулы:

Среднее арифметическое :

Выборочная медиана:

Середина размаха:

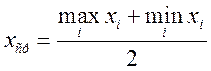
Центральные моменты вычисляем по формуле:

2.1.2  Асимметрии и эксцесса

Асимметрия:

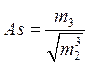
Эксцесс:

Результаты представлены в таблице:

Таблица 1

					s			As	Ex
2000	15,229	15,456	15	12,3987	3,52118	-4,1421	232,304	-0,0948	1,5111
200(1)	15,347	15,555	14,998	77,2028	8,78651	-2,5874	213,600	-0,0038	0,0358
200(2)	15,382	16,312	15,000	73,5787	8,57780	-2,0059	235,864	-0,0031	0,0435
200(3)	14,819	14,945	15,001	79,3141	8,90585	-11,227	223,606	-0,015	0,0355
200(4)	15,331	16,026	15,000	79,4156	8,91154	-2,2818	257,172	-0,003	0,0407
200(5)	15,556	16,163	14,999	78,0031	8,83194	2,59939	223,328	0,0037	0,0367
200(6)	15,273	15,339	15,000	74,6687	8,64110	-1,7120	229,758	-0,0026	0,0412
200(7)	15,272	15,427	15,000	73,6198	8,58020	-1,9892	236,35	-0,0031	0,0436
200(8)	14,961	14,910	15,000	86,6166	9,30680	-11,514	239,498	-0,0142	0,0319
200(9)	15,081	15,015	14,997	82,1567	9,06403	-8,4858	249,772	-0,0114	0,0370
200(10)	15,271	15,407	14,999	83,5138	9,13859	-2,2168	214,085	-0,0029	0,0306

Графическое представление результатов

Оценки м. о.

<x>

x_med

x_ср

Оценки дисперсии

Оценки третьего центрального момента

Оценки четвёртого центрального момента

Оценки асимметрии

Оценки эксцесса

Рис.3 Графическое представление результатов

2.1.3  Границ интерквантильного промежутка  для P=0.95 только по полной выборке.

2.2  Интервальные оценки с доверительной вероятностью Q :

Доверительный интервал для первого начального момента (математического ожидания) определяется из неравенства 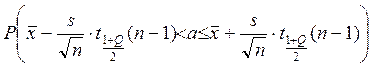, где

 - точечная несмещенная оценка математического ожидания;

 - точечная несмещенная оценка дисперсии;

 - квантиль плотности распределения Стьюдента с -ой степенью свободы.

Считая, что выборка извлечена из нормальной генеральной совокупности, доверительный интервал для дисперсии будет определятся из неравенства 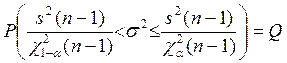, где

 - точечная несмещенная оценка дисперсии;

 и  - квантили плотности распределения “хи-квадрат”.

Доверительный интервал для интерквантильного промежутка  для P=0.95 определялся несколькими способами: