Построение выборочной функции распределения. Гистограмма. Точечные оценки моментов, страница 2

С помощью непараметрических толерантных пределов, симметричных относительно математического ожидания. Количество отбрасываемых статистически эквивалентных блоков k определяется из неравенства .

Для доверительной вероятности Q=0.8 и объема выборки N=2000 это количество k=176, то есть границы доверительного интервала равны и .

При оценке с помощью непараметрических толерантных пределов, несимметричных относительно математического ожидания. В этом случае толерантными пределами являются значения  и

При оценке доверительного интервала по частичным выборкам, состоящим из 200 значений с помощью параметрических толерантных пределов, границы интерквантильного промежутка равны , где

 - точечная несмещенная оценка математического ожидания;

 - точечная несмещенная оценка дисперсии;

 - толерантный множитель.

Для P=0.95 и Q=0.8 =1,9872 при N=2000 и 2.0543 для N=200.

Графическое представление результатов

Первый начальный момент

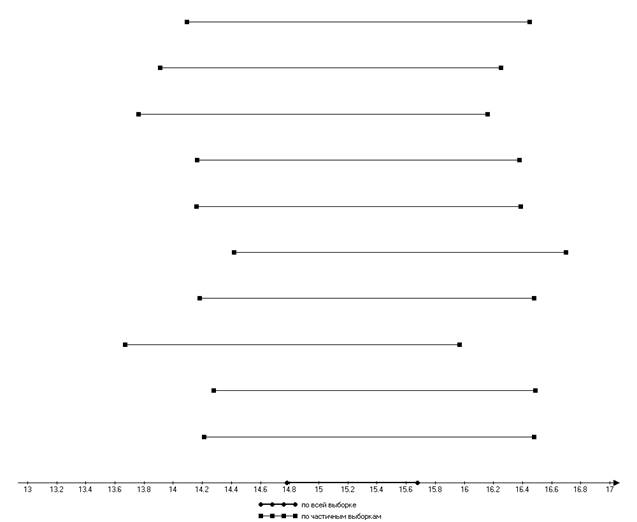
Второй центральный момент

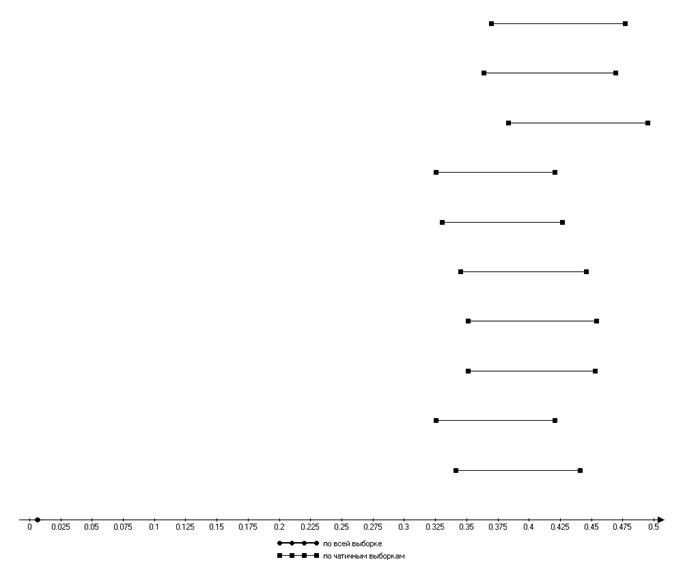
Интерквантильный промежуток

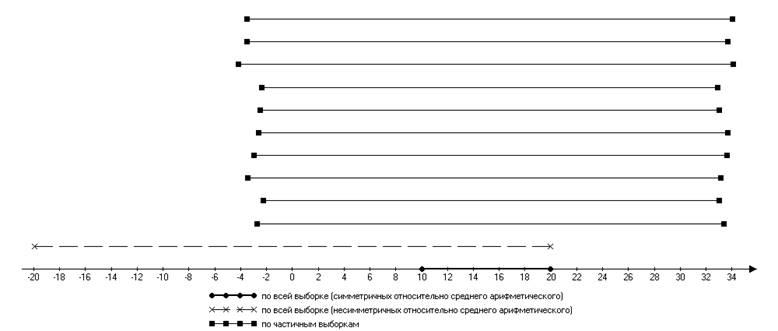
Рис.4 Графическое представление результатов

3.  Идентифицировать закон распределения и выбрать подходящий

Зададим уровень значимости α=0,05

Учитывая посчитанные значения эксцесса и моментов, а также вид полученной гистограммы, предположим, что наше распределение арксинус. Проверим эту гипотезу по трем критериям.

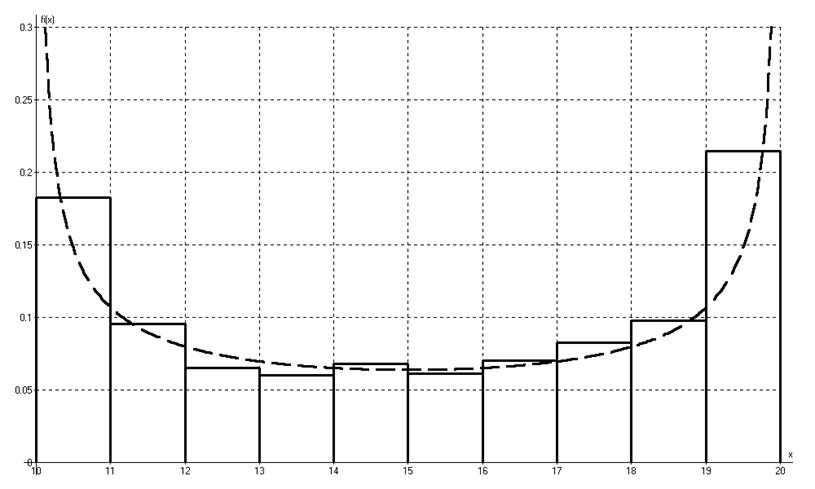
Рис. 5 Гистограмма и теоретический закон распределения (арксинус)

Проверка по критерию «хи-квадрат»

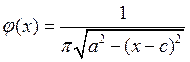
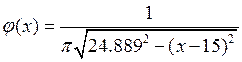
Вычислим статистику критерия по формуле 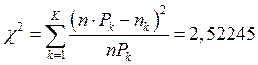,  - где ожидаемое число попаданий в k-ый интервал, а  - количество наблюдений в j-м интервале

Найдем по таблице критическое значение .

Поскольку  можно сказать, что экспериментальные данные не противоречат выдвинутой гипотезе.

Проверка по критерию Колмогорова-Смирнова

Мера расхождения между предполагаемой и выборочной функцией распределения

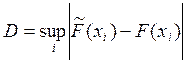
Критическое значение (табличное) D_α = 0,007792 при α=0,05. Получено следующее значение критерия D = 0,003951 < D_α. 

Так как полученное значение меньше критического, нашу гипотезу можно считать справедливой.

Проверка по критерию Мизеса ( «омега-квадрат» )

Мера расхождения между предполагаемой и выборочной функцией распределения

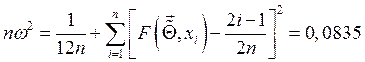
Критическое значение (табличное)  =0,4614  при α  = 0.05

Получено следующее значение критерия   =  <

Все три критерия подтвердили гипотезу. Так как все гипотезы оказались справедливы, можем говорить, что у нас достаточно оснований чтобы не отклонять предположение, что наше распределение арксинус.

Часть 2

Исходные данные:

nx = 6  ny = 10

Таблица 2

	-5	-3	-1	1	3	5
1	-135,714798	6,046753	21,092802	9,069806	23,25276	150,74948
2	-118,06929	-2,526779	23,957058	4,648707	27,363121	150,58502
3	-120,68045	0,302362	23,269936	1,763046	22,552149	149,3577
4	-126,771667	10,119068	20,849598	2,418877	23,082308	150,78033
5	-122,976089	-0,82746	19,99905	4,828962	22,985651	151,28485
6	-127,623856	4,684571	19,188438	2,35134	19,163033	148,55718
7	-129,840012	5,810667	23,848412	6,406444	25,743412	148,7395
8	-132,242004	0,641584	21,897274	5,510309	22,577435	151,22258
9	-126,078224	6,794114	19,720289	8,813305	25,180569	149,20186
10	-119,913147	1,479867	26,206783	1,998635	24,664013	149,856

1.  Вычисления.

1.1  В каждой точке  средние арифметические значения , оценки дисперсий , параметрические толерантные пределы для погрешностей, доверительные интервалы для математических ожиданий, проверить гипотезу о равенстве дисперсий в этих точках по критерию Кочрена