Построение выборочной функции распределения. Гистограмма. Точечные оценки моментов, страница 3

В каждой точке x_i средние арифметические значения y, оценки дисперсий (табл. 2.1).

 ,

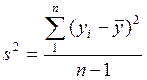
Таблица 2.1

Параметрические толерантные пределы для погрешностей (табл. 2.2):

J(P,Q) = [-(n,P,Q); +(n,P,Q)], где 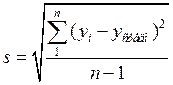 - оценка среднеквадратического отклонения, толерантный множитель для  n=10; Q=0,8: k(n,0.95,Q) = 2,69

Доверительные интервалы для математических ожиданий y (табл. 2.2):

Коэффициент Стъюдента для  Q=0,8; n = 10: =1,38

Таблица 2.2

xi	-5	-3	-1	1	3	5
s	32,078986	16,08936	5,091014	7,353286	4,994452	1,043129

Толерантные пределы J(P,Q)
н	-141,2267	-7,53753		15,93344	-2,51351	17,64476	147,2861
в	-110,7552	14,04248		28,07249	12,0754	29,66813	152,7808
Доверительные интервалы для математического ожидания
н	-128,4626		1,50203	21,01832	3,597575	22,68118	149,5877
в	-123,5193		5,00292	22,98761	5,964311	24,63171	150,4792

Проверка гипотезы о равенстве дисперсий в этих точках по критерию Кочрена.

Гипотеза: H₀  - считаем, что измерения равноточные.

Значение критерия Кочрена 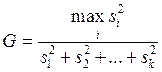, для k=6, n=10, уровень значимости =0,05:

G = 0,4813035, критическое значение критерия  = 0,3682.

G > , следовательно, у нас нет достаточных оснований для того, чтобы считать нашу гипотезу справедливой, измерения выходной величины считаем неравноточными. Дальнейшая обработка данных будит поводиться по методу наименьшей дисперсии (МНД).

Результаты предварительной обработки исходных данных в виде вектора средних значений и матрицы оценок дисперсии:

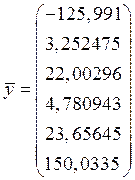
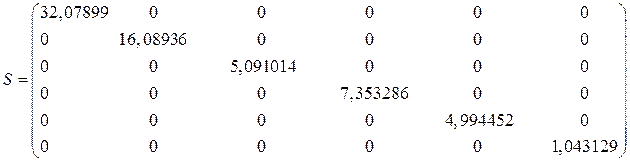
1.2  Оценки коэффициентов полинома МНД

Степень полинома a-priori не известна, принимаем q=1.

, i = 1,2, … n

матричный вид:

            Матрица X и вектор A имеют вид:

 

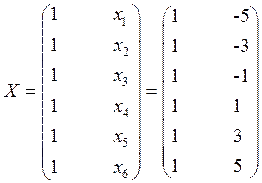
Вектор оценок коэффициентов полинома:

1.3  Проверка гипотезы о степени полинома.

Предположение: гипотеза: степень полинома q=1; Альтернатива: q>1;

Сформулированная гипотеза проверяется с помощью упрощённого критерия Фишера. Значение критерия:

, уровень значимости =0,05.

R=1.5811e+004;

Проверка критерия сводится к проверке неравенства:

, где k-q-1=6-1-1=4, n-1=9;

Критическое значение критерия Фишера =3,63;

Неравенство не выполняется.

Выбранная степень полинома недостаточна, т. е. q>1.

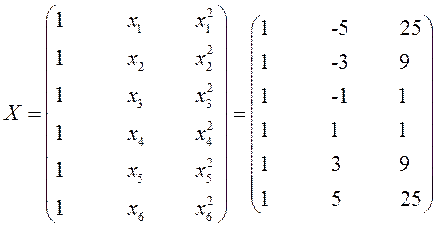
Принимаем q=2.

Матрица X и вектор A имеют вид:

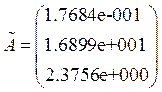
Проверка гипотезы о степени полинома.

Предположение: гипотеза: степень полинома q=2; Альтернатива: q>2;

R=1.1795e+004;

Критическое значение критерия Фишера =3,86;

Неравенство не выполняется.

Выбранная степень полинома недостаточна, т. е. q>2.

Принимаем q=3.

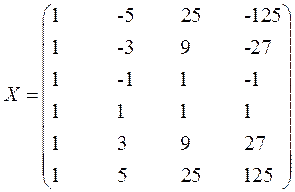
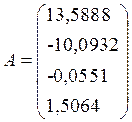
Проверка гипотезы о степени полинома.

Предположение: гипотеза: степень полинома q=3; Альтернатива: q>3;

R= 3.5622e-001;

Критическое значение критерия Фишера =4,26;

Неравенство  выполняется.

Гипотеза не противоречит экспериментальным данным.

Полученная аппроксимирующая полиномиальная функция:

Оценка дисперсии и ковариации оценок коэффициентов.

 - дисперсионная матрица оценок коэффициентов:

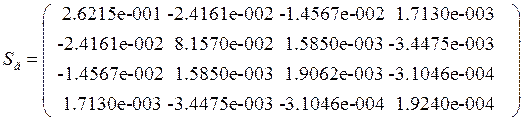
Число обусловленности матрицы cond()= 4.3216e+004.

Вычисление коэффициентов корреляции между оценками коэффициентов.

Коэффициенты корреляции: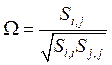  

Корреляционная матрица:

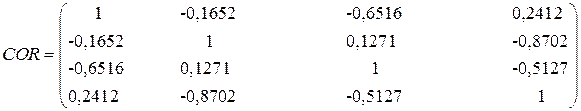
Оценки коэффициентов полинома для q=k-1=5 (вычисление коэффициентов корреляции между оценками коэффициентов ).

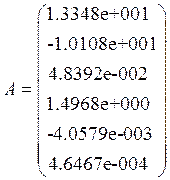
Дисперсионная матрица оценок коэффициентов:

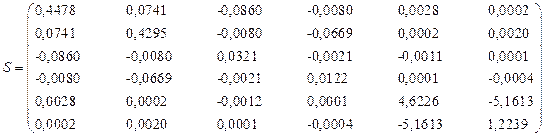
Число обусловленности матрицы cond(S)= 5.3006e+007.

Корреляционная матрица:

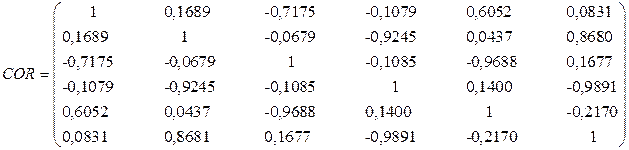
Графическое представление результатов

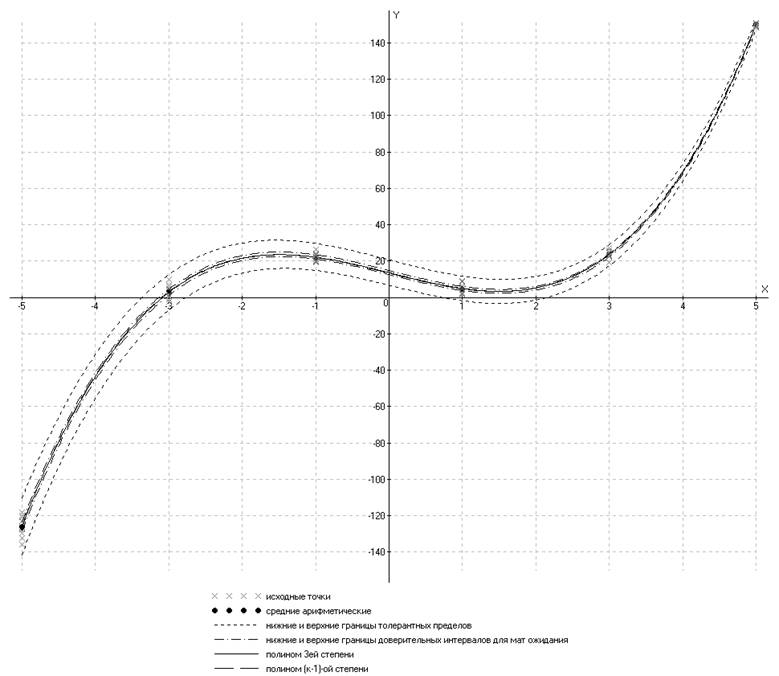
Рис.6 Графическое представление результатов