Построение выборочной функции распределения. Асимметрия и эксцессы. Выборочная медиана

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Расчетное задание №2

по теории вероятностей

Вариант 2

Преподаватель:

Выполнил:

студент  гр. 2083/2

САНКТ-ПЕТЕРБУРГ 2009 г.

РАЗДЕЛ I

В результате измерений получена выборка   из генеральной совокупности с неизвестным законом распределения

1. Построить :

   1.1 Выборочную функцию распределения F(x)

  1.2 Гистограмму

2. Вычислить :

2.1 Точечные оценки :

 2.1.1 моментов

Для  оценки первого начального момента использовать следующие способы:

Среднее арифметическое :

Выборочная медиана:

Середина размаха:

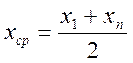
Центральные моменты вычисляем по формуле:

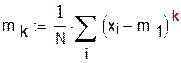
 2.1.2 асимметрии и эксцесса

асимметрия:

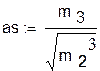
эксцесс:

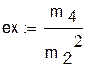
Результаты представлены в таблице:

n							As	ex
100	1.657	1.5852	1.9636	16.096	11.8906	574.2742733	0.18693	2.2616
10	2.205	0.775	2.453	20.366	29.671	685.859	11.218	2.041
10	2.523	1.864	3.79	13.523	26.306	353.475	16.299	2.386
10	2.443	3.156	1.108	5.951	-14.302	87.299	16.503	3.043
10	1.292	-0.896	2.714	28.075	83.022	1.133*10^3	54.268	1.775
10	1.794	1.806	2.189	19.927	16.714	558.748	3.678	1.737
10	2.074	2.53	1.865	7.64	-2.291	96.656	0.291	2.044
10	-0.343	-1.022	0.704	15.66	27.051	368.672	13.83	1.856
10	1.869	2.106	1.497	23.285	-1.625	894.359	0.028	2.037
10	1.033	0.393	0.277	16.157	-11.864	391.013	2.538	1.849
10	1.676	2.813	2.152	19.331	7.725	833.327	0.822	2.753

Графическое представление результатов:

Оценка математического ожидания:

Оценка дисперсии:

Оценка третьего центрального момента :

Оценка четвертого центрального момента :

Оценка асимметрии:

Оценка эксцесса:

   2.1.3 границ интерквантильного промежутка  для P=0.95 только по полной выборке.

Генеральными граничными квантилями этого промежутка являются x_(1-P)/2  и x_(1+P)/2  

По выборочной функции распределения были найдены:

x_(1-P)/2  = -5.681          x_(1+P)/2  = 9.614

2.2. Интервальные оценки с доверительной вероятностью Q=0.8 :

Доверительный интервал для первого начального момента (математического ожидания) определяется из неравенства 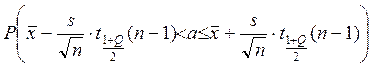, где

 - точечная несмещенная оценка математического ожидания;

 - точечная несмещенная оценка дисперсии;

 - квантиль плотности распределения Стьюдента с -ой степенью свободы.

Считая, что выборка извлечена из нормальной генеральной совокупности, доверительный интервал для дисперсии будет определятся из неравенства 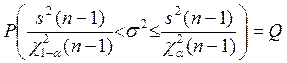, где

 - точечная несмещенная оценка дисперсии;

 и  - квантили плотности распределения “хи-квадрат”.

Доверительный интервал для интерквантильного промежутка для P=0.95 определялся несколькими способами:

1.С помощью непараметрических толерантных пределов, симметричных относительно математического ожидания. Количество отбрасываемых статистически эквивалентных блоков k определяется из неравенства .

Для доверительной вероятности Q=0.8 и объема выборки N=100 это количество k=2, то есть границы доверительного интервала равны и

С помощью непараметрических толерантных пределов, симметричных относительно начала координат. В этом случае толерантными пределами являются значения  и