Математика \ Теория вероятностей, математическая статистика и основы теории случайных процессов

Построение выборочной функции распределения. Асимметрия и эксцессы. Выборочная медиана, страница 2

Поскольку для непараметрических толерантных пределов при заданной вероятности Q=0.8 минимально необходимый объем выборки больше либо равен 32 (как для симметричных относительно математического ожидания, так и для симметричных относительно начала координат), то для оценки доверительного интервала по частичным выборкам, состоящим из 10-ти значений, используются параметрические толерантные пределы (при этом считается, что выборка извлечена из нормальной генеральной совокупности). Границы интерквантильного промежутка в этом случае равны ,где

 - точечная несмещенная оценка математического ожидания;

 - точечная несмещенная оценка дисперсии;

 - толерантный множитель.

Толерантный множитель можно найти по таблице, либо вычислить его приближенно по формул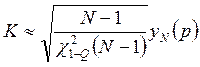е , где

 - квантиль плотности распределения “хи-квадрат”;

 - решение уравнения , а

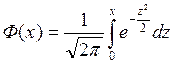 - функция Лапласа.

Для P=0.95 и Q=0.8 =2.101 при N=100 и 2.656775626 для N=10.

Графическое представление результатов

На всех графиках на оси x представлен доверительный интервал для полной выборки, а выше нее – доверительные интервалы для 10 частичных выборок.

Первый начальный момент:

Второй центральный момент :

Интерквантильный промежуток:

-1   симметричный относительно математического ожидания

-2   симметричный относительно начала координат

3. Идентифицировать закон распределения и выбрать подходящий

Исходя из формы гистограммы, асимметрии выдвигаем гипотезу Н0, что рассматриваемая выборка извлечена из нормально распределенной генеральной совокупности. Кривая нормальной плотности распределения описывается функцией 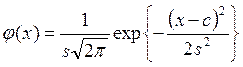, где

 - точечная оценка математического ожидания; с=1,657

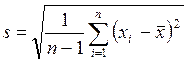 - точечная оценка среднеквадратичного отклонения. s=4,012

Графическое построение:

Проверим гипотезу о соответствии предполагаемого закона распределения экспериментальным данным с помощью трех критериев: “хи-квадрат”, Колмогорова-Смирнова, “омега-квадрат” Мизеса. Примем уровень значимости . Тогда для каждого из трех критериев первые пять пунктов проверки уже реализованы: задан уровень значимости, построены гистограмма и выборочная функция распределения, вычислены точечные оценки моментов, выдвинута гипотеза о виде плотности и функции распределения и вычислены оценки параметров предполагаемых функций.


Критерий “хи-квадрат”.

Вычислим статистику критерия по формуле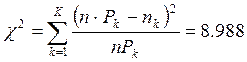

Найдем критическое значение  (K=11 – количество столбцов гистограммы, r=2 – количество оцениваемых параметров).

Поскольку  можно сказать, что экспериментальные данные не противоречат выдвинутой гипотезе Н0.

     Критерий Колмогорова-Смирнова

Вычислим статистику критерия:

Критическое значение критерия для и N=100 находим в таблице:

, следовательно, экспериментальные данные не противоречат  выдвинутой гипотезе Н0 .

   Критерий “омега-квадрат” Мизеса

Вычислим статистику критерия: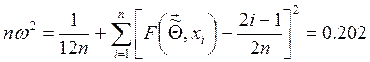

Критическое значение критерия для  находим в таблице:

, следовательно, экспериментальные данные не противоречат    выдвинутой гипотезе Н0 .

Так как гипотеза о виде функции и плотности распределения не противоречит  всем  рассмотренным критериям, то ее можно принять.

Раздел II

Оценивание методом наименьших квадратов (МНК) и методом наименьшей дисперсии (МНД) коэффициентов полиномов, аппроксимирующих результаты измерений зависимых переменных.

В каждой точке xi   были вычислены средние арифметические значения

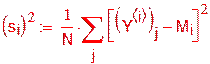
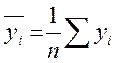, оценки  дисперсий доверительные интервалы для математических ожиданий из неравенства

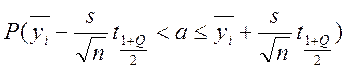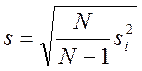,где -точечная несмещенная оценка дисперсии;

Проверим гипотезу о равенстве дисперсий в точках по критерию Кочрена:

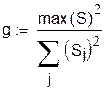Вычислим статистику критерия: , g = 0.204652

Критическое значение критерия для α=005,n=10 и k=12 находим в таблице gкр=0.2098

g<gкр .

последовательная полиномиальная аппроксимация с проверкой гипотезы о степени полинома:

Статистика критерия проверки гипотезы о степени полинома:

Критические значения плотности распределения Фишера были найдены в таблицах.

p

k-p-1

Fp

Fкр

1

10

34.9772

3.71

2

9

31.7572

3.63

3

8

0.4377

3.69

Тат как степень полинома не известна необходимо было начать попытки аппроксимации с наименьшей степени и проверять гипотезу о степени полинома. На третьем шаге гипотеза не была отвергнута.

При этом вычисленные коэффициенты равны

Вычислим ковариационную матрицу погрешностей определения коэффициентов аппроксимирующего полинома по формуле:

Вычислим коэффициенты корреляции между оценками коэффициентов:

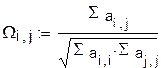
Все точки:
Скачать файл