1.7. Двумерные непрерывные случайные величины
(двумерные векторы)
1.7.1. Функции распределения и плотности распределения
Будем рассматривать двумерный случайный вектор, то есть двумерный вектор, каждая составляющая которого есть непрерывная случайная величина:
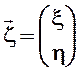 .
.
Как и ранее, случайный
вектор и его случайные компоненты мы обозначаем греческими буквами, а значения,
которые может принимать вектор и его компоненты, будем обозначать
соответствующими латинскими буквами, то есть будем считать, что случайный
вектор ![]() принимает значения
принимает значения
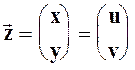 .
.
Функция распределения двумерного случайного вектора есть вероятность совместного осуществления событий:
![]()
Плотность распределения, как и ранее, есть производная от функции распределения по обоим аргументам:
|
|
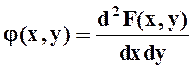 , поэтому
, поэтому
 .
.
Область интегрирования показана на рис. 23.
В силу монотонности вероятностной меры функция распределения - неубывающая функция по каждому аргументу, а потому плотность распределения есть неотрицательная функция двух аргументов, которая описывает некоторую поверхность над координатной плоскостью. Эта поверхность приближается к плоскости XOY при удалении значений аргументов от начала координат по любому направлению. Понятно, что
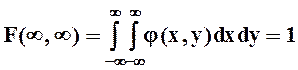 .
.
Если по одному из аргументов ограничений нет, то
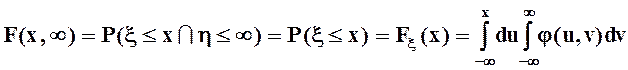 .
.
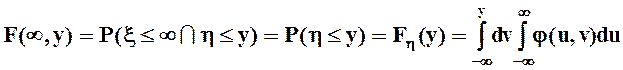 .
.
Таким образом мы получили
маргинальные (частные) функции распределения ![]() и
и ![]() . Дифференцирование этих функций по их аргументам, то есть
дифференцирование соответствующих интегралов по их верхним пределам, по
определению, дает маргинальные (частные) плотности распределения:
. Дифференцирование этих функций по их аргументам, то есть
дифференцирование соответствующих интегралов по их верхним пределам, по
определению, дает маргинальные (частные) плотности распределения:
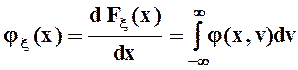 ,
, 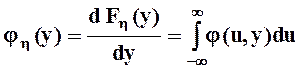 .
.
|
|
Определим условную функцию распределения, то есть функцию распределения одной из случайных величин при условии, что другая случайная величина принимает некоторое конкретное значение, например,
![]() .
.
Выделим на координатной плоскости область, показанную на рис. 24.
Вероятность того что
случайный вектор принимает значения из этой области, равна ![]() . В соответствии с формулой для
условной вероятности из п. 1.2.3
. В соответствии с формулой для
условной вероятности из п. 1.2.3
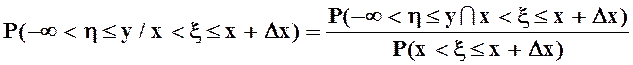 .
.
Условная функция распределения получается в результате предельного перехода:
![]()
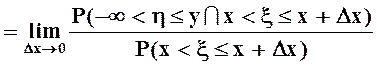
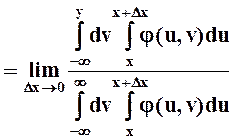 .
.
По теореме о среднем,
внутри интервала ![]() найдется точка
найдется точка ![]() , такая, что
, такая, что
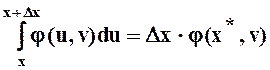 , поэтому
, поэтому
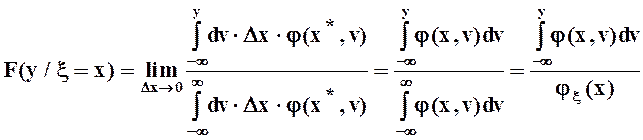 .
.
Условная плотность распределения есть производная от условной функции распределения:
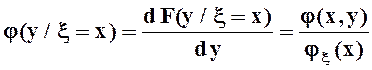 .
.
Аналогично
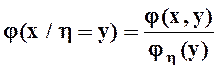 .
.
Обычно обозначают ![]() и
и ![]() . В этих обозначениях из полученных формул следует:
. В этих обозначениях из полученных формул следует:
![]() ,
, ![]() .
.
С учетом полученных соотношений перепишем формулы для маргинальных распределений в виде:
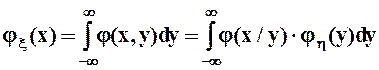 ,
, 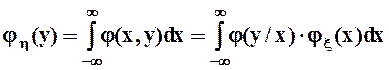 .
.
Это формулы полной вероятности для непрерывных случайных величин.
Поскольку ![]() =
= ![]() , получаем формулу Байеса для
непрерывных случайных величин:
, получаем формулу Байеса для
непрерывных случайных величин:
 .
.
Если x и h независимы, то ![]() ,
, ![]() и поэтому
и поэтому ![]() .
.
Справедливо и обратное,
то есть, если ![]() , то из этого с необходимостью
следует независимость x
и h.
, то из этого с необходимостью
следует независимость x
и h.
Признак независимости случайных величин: две случайные величины независимы тогда и только тогда, когда их совместная плотность распределения может быть представлена, как произведение маргинальных плотностей распределения этих величин (см. также п. 1.2.3).
1.7.2.Числовые характеристики
Моменты случайных величин определяются, как и ранее, формулами
- начальные моменты k - го порядка :
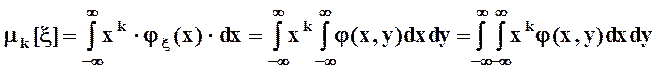 ,
,
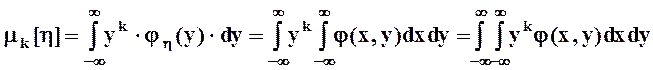 .
.
- центральные моменты k - го порядка:
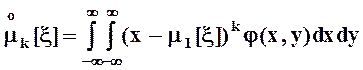 ,
, 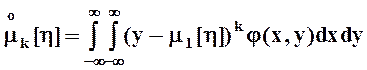 .
.
Среди этих моментов
самыми употребительными являются математические ожидания ![]() и дисперсии
и дисперсии ![]() ,
, ![]() . Математическое
. Математическое ![]() ожидание случайного вектора есть вектор, компонентами
которого являются математические ожидания соответствующих составляющих:
ожидание случайного вектора есть вектор, компонентами
которого являются математические ожидания соответствующих составляющих:
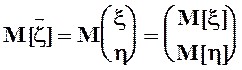 .
.
Из условных моментов выделим лишь первые начальные (условные математические ожидания) и вторые центральные (условные дисперсии):
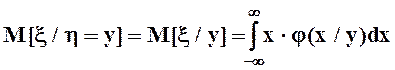 ,
, 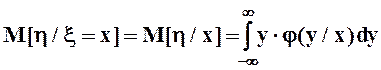 ,
,
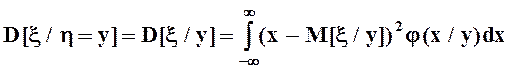 ,
,
 .
.
Как и ранее, во всех случаях
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Для двумерных случайных величин вводятся смешанные моменты:
- начальные порядка k, r
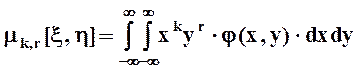 ,
,
-центральные порядка k, r
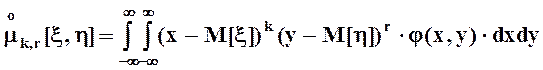 .
.
Из них наиболее употребительным является центральный смешанный момент порядка (1, 1), который называется ковариацией и обозначается, как cov(x, h):
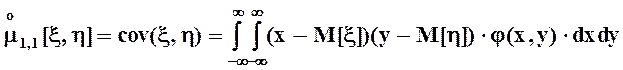 .
.
Выясним связь между этим и начальным смешанным моментом того же порядка.
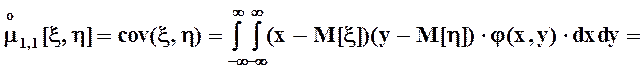
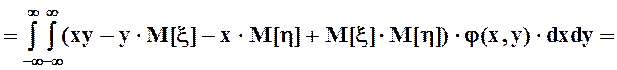
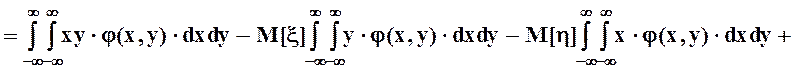
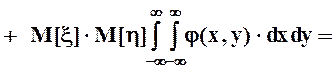
![]() .
.
В итоге получаем, что ![]()
![]()
Если случайные величины x и hнезависимы, в соответствии с признаком независимости, сформулированным выше,
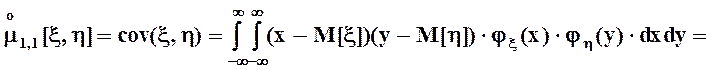
=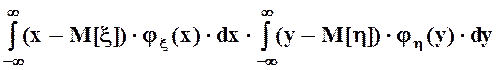 , то есть мы видим, что двукратный
интеграл в этих условиях преобразуется в произведение однократных интегралов, каждый из которых равен нулю. В самом деле,
, то есть мы видим, что двукратный
интеграл в этих условиях преобразуется в произведение однократных интегралов, каждый из которых равен нулю. В самом деле,
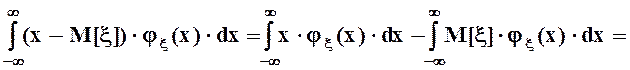
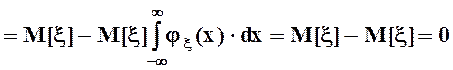 .
.
Поэтому при условии независимости случайных величин x и hих первый центральный смешаный момент или ковариация равна 0.
В случае взаимнооднозначной зависимости между x и h, например, линейной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.