Передаточную функцию
звена (системы автоматического управления) ![]() можно
преобразовать, разложив на множители полиномы ее числителя и знаменателя.
Конечно, если известны корни уравнений
можно
преобразовать, разложив на множители полиномы ее числителя и знаменателя.
Конечно, если известны корни уравнений ![]() (нули)
и
(нули)
и ![]() (полюса).
(полюса).
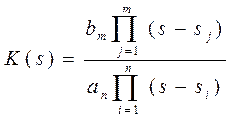 .
.
Если в передаточной
функции произвести замену ![]() , то
получаем
, то
получаем 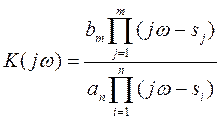 , называемое частотной
характеристикой звена (частотный , комплексный коэффициент передачи звена, АФХ).
, называемое частотной
характеристикой звена (частотный , комплексный коэффициент передачи звена, АФХ).
Общая фаза выходного сигнала звена будет складываться из частичных фаз, определяемых каждым двучленом числителя и знаменателя. Об этом будет более подробно в соответствующем разделе ниже.
Корни полиномов
числителя и знаменателя ![]() можно
изобразить на плоскости.
можно
изобразить на плоскости.
Комплексная плоскость
корней ![]() и
и ![]() :
:
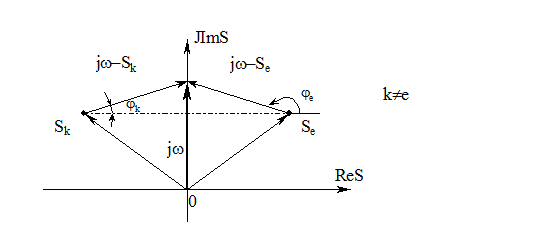
Отсюда:
1. Корень ![]() расположен в правой
полуплоскости, то есть ReSe>0 .
расположен в правой
полуплоскости, то есть ReSe>0 .
2. Корень ![]() расположен в левой
полуплоскости, то есть ReSk<0 .
расположен в левой
полуплоскости, то есть ReSk<0 .
3. Углы наклона векторов ![]() и
и ![]() таковы, что jk<je, причем
таковы, что jk<je, причем
![]() ,
, ![]() .
.
Звено, у которого все корни (полюса и нули) расположены в левой полуплоскости (являются левыми) называется минимально фазовым звеном.
Если хотя бы один из корней звена расположен справа, то такое звено - не минимально фазовое звено.
У минимально фазовых звеньев существует однозначная зависимость между их частотными характеристиками.
То есть, располагая одной частотной характеристикой, можно построить остальные. Другими словами, в любой частотной характеристике заключена вся информация о поведении звена.
Неустойчивые звенья - всегда не минимально фазовые.
Все многообразие звеньев может быть по математическому описанию представлено лишь несколькими характерными (типовыми) звеньями.
Минимально фазовые звенья:
1. Идеальное усилительное звено (пропорциональное безинерционное, усилительное, звено нулевого порядка);
2. Реальное усилительное звено (апериодическое, инерционное первого порядка);
3. Идеальное дифференцирующее звено;
4. Реальное дифференцирующее звено;
5. Идеальное интегрирующее звено (интегратор);
6. Идеальное форсирующее звено;
7. Звенья второго порядка:
· Апериодическое (вообще-то это комбинация двух апериодических звеньев первого порядка);
· Колебательное;
· Консервативное.
Не минимально фазовые звенья:
1. Звено чистого запаздывания (особое звено с неограниченным изменением фазы);
2. Квазиапериодическое звено;
3. Квазиколебательное звено.

Это делитель напряжения, реостат - идеальное звено, если пренебречь его индуктивностью.
Получим частотные
характеристики идеального усилительного звена. Заменяем в передаточной функции ![]() :
: ![]() ;
;
Тогда ВЧХ и МЧХ звена будут
определяться как ![]() ;
; ![]() ;
;
Фазо-частотная характеристика
ФЧХ звена: 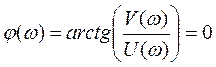 ;
;
Амплитудо-частотная
характеристика АЧХ: ![]() ;
;
Логарифмическая амплитудная (амплитудо-частотная)
характеристика ЛАХ звена: ![]() .
.
Переходная характеристика ![]() ℒ
ℒ![]() .
.
Весовая функция (импульсная
переходная характеристика) ![]() .
.
Все характеристики идеального усилительного звена изображены на рисунках:
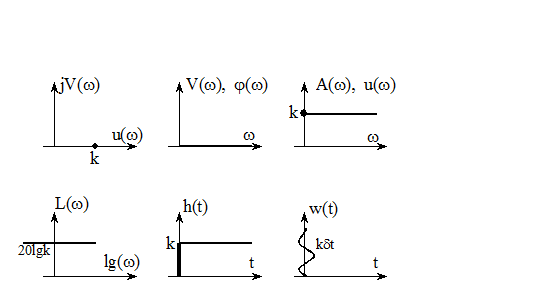
В электромеханических системах типичным примером идеального усилительного (безинерционного) звена является датчик – преобразователь скорости вращения в напряжение, – тахогенератор.
Математические модели данного звена имеют вид:
дифференциальное уравнение: ![]() ; соответствующая ему
передаточная функция:
; соответствующая ему
передаточная функция: ![]() ;
частотные характеристики:
;
частотные характеристики:
![]() -
АФЧХ;
-
АФЧХ;
![]() -
ВЧХ;
-
ВЧХ; ![]() - МЧХ; причем
- МЧХ; причем ![]() ,
, ![]() .
.
Следовательно, ![]() (АФЧХ) располагается в
четвертом квадранте координатной плоскости. Кроме того
(АФЧХ) располагается в
четвертом квадранте координатной плоскости. Кроме того ![]() (выполнили деление). Если
подставить
(выполнили деление). Если
подставить ![]() в
в ![]() , то получим
, то получим 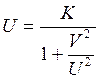 , откуда после преобразований:
, откуда после преобразований:
![]() ;
Þ
;
Þ 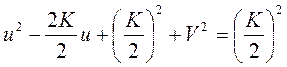 ;
Þ
;
Þ 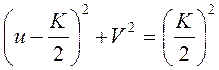 .
.
Имеем окружность радиусом ![]() , сдвинутую на
, сдвинутую на ![]() вправо по оси абсцисс.
вправо по оси абсцисс.
Можно утверждать, что АФЧХ расположена, как показано на рис.:
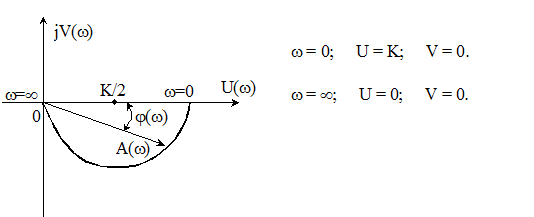
Амплитудо-частотная
характеристика реального усилительного звена имеет вид: ![]()
Фазо-частотная характеристика: ![]() , причем
, причем ![]() ,
, ![]() .
.
На графиках представлены все полученные зависимости:
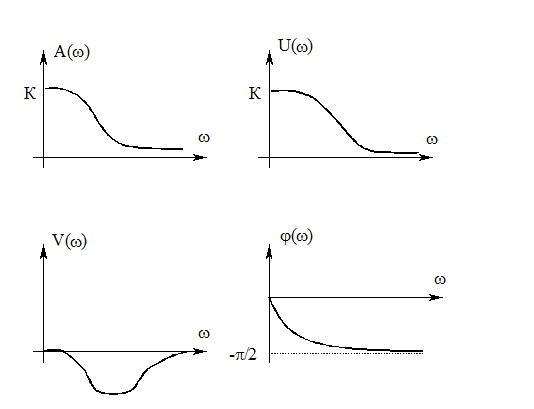
Логарифмическая амплитудо-частотная характеристика (ЛАХ):
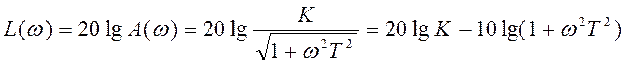 .
.
Для ее построения выполним исследования. а) Зона низкой частоты. Н.Ч.
![]() ,
,
![]() .
.
б) Зона высокой частоты. В.Ч.
![]() ,
,
![]() ;
; ![]() ;
;
Наклон характеристики в области
высоких частот ![]() .
.
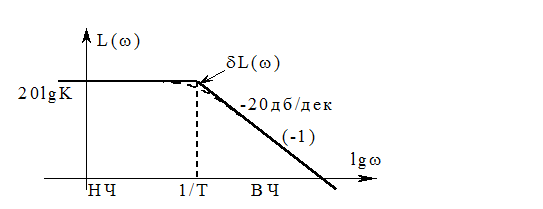
Изображенная на рис. логарифмическая характеристика в виде кусочно-ломаной линии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.