Определение параметров автоколебаний НСАУ. Идентификация объекта управления. Схема эксперимента

Санкт-Петербургский Государственный Политехнический Университет

___________________________________________________ Факультет Технической Кибернетики Кафедра Систем Автоматического Управления

Отчет по лабораторной работе №3

«Определение параметров автоколебаний НСАУ»

Выполнили:       

Группа:           4083/2

Преподаватель:     

Санкт-Петербург

2005 год

1.  Идентификация объекта управления.

Схема эксперимента:

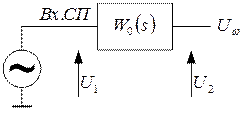
В ходе эксперимента получаем таблицу:

0,1	20	5,200	0,63	-0,20	0,2600	-11,70
0,2	20	5,200	1,26	0,10	0,2600	-11,70
0,4	20	5,200	2,51	0,40	0,2600	-11,70
0,8	20	5,200	5,03	0,70	0,2600	-11,70
1	20	5,200	6,28	0,80	0,2600	-11,70
2	20	4,800	12,57	1,10	0,2400	-12,40
4	20	3,800	25,13	1,40	0,1900	-14,42
8	20	2,600	50,27	1,70	0,1300	-17,72
10	20	2,000	62,83	1,80	0,1000	-20,00
20	20	0,850	125,66	2,10	0,0425	-27,43
40	20	0,220	251,33	2,40	0,0110	-39,17
80	20	0,042	502,65	2,70	0,0021	-53,56
100	20	0,020	628,32	2,80	0,0010	-60,00
200	20	0,004	1256,64	3,10	0,0002	-73,98

Расчетные формулы:

, , .

ЛАХ объекта управления

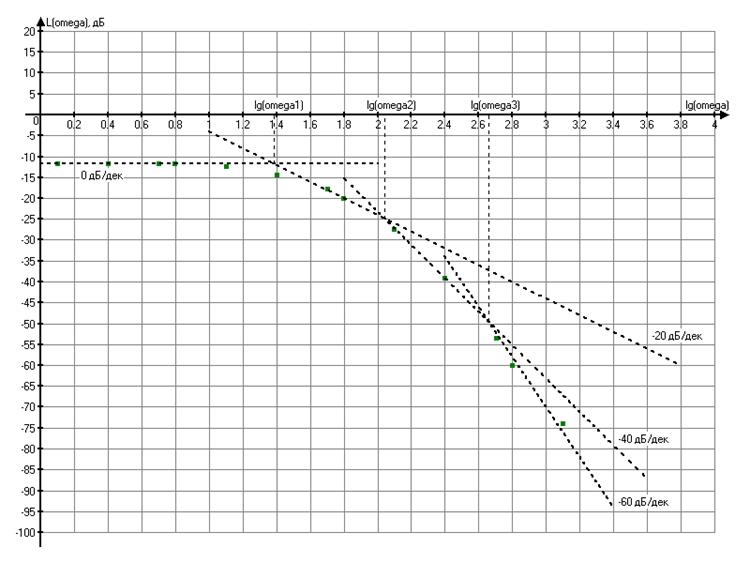
Предполагается, что объект управления можно заменить на три последовательно соединённых апериодических звена, значит коэффициент передачи его будет равен:

.

Для нахождения конкретных значений, аппроксимируем полученную ЛАХ четырьмя прямыми с наклонами 0 дБ/дек, -20 дБ/дек, -40 дБ/дек, -60 дБ/дек.

Из графика получены следующие значения параметров объекта:

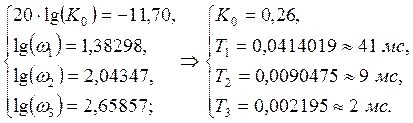
2.  Исследование замкнутой системы.

Схема эксперимента:

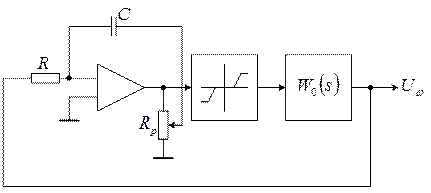
Параметры нелинейного элемента:

·  Зона нечувствительности: ,

·  Насыщение: .

Параметры интегратора:

Теоретические параметры:

,

.

Практические параметры:

,

.

В качестве нелинейного звена используется элемент с зоной нечувствительности и с насыщением. Регулируя потенциометр, добиваемся автоколебаний и фиксируем период колебаний и двойную амплитуду:

,    .

Измерим значение , как отношение выходного напряжения к входному:

.

Таким образом получаем:

.

3.  Теоретическая часть.

Структурная схема выглядит следующим образом:

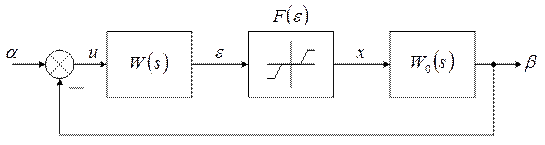
Эта система определяется следующими уравнениями:

,    , ,   .

Здесь объект управления представляет собой систему третьего порядка со следующей передаточной функцией:

, где

 - коэффициент пропорциональности непосредственно объекта управления;

, ,  - постоянные времени объекта управления.

А также в системе присутствует интегрирующее звено:

.

Нелинейная часть представляет собой звено с насыщением и зоной нечувствительности, параметры которых приведены выше. После гармонической линеаризации нелинейность даёт следующую зависимость:

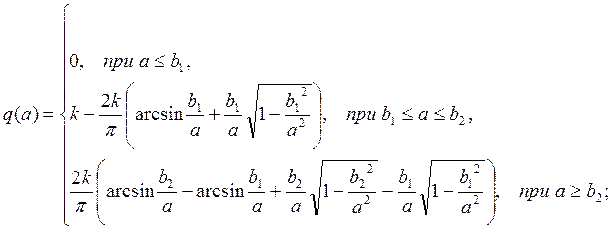
Или, подставляя конкретные значения:

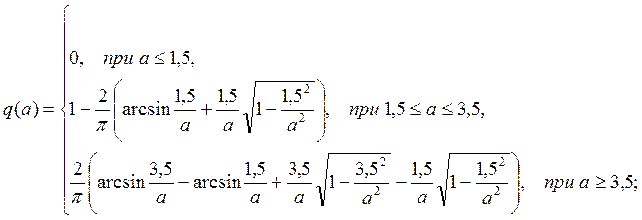
Тогда гармонически линеаризованное уравнение замкнутой системы при , будет выглядеть:

, а характеристическое уравнение:

.

Если подставить  и разбить на действительную и мнимую части, получим:

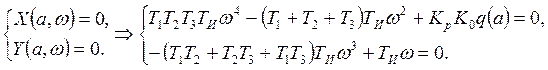
Из второго уравнения получаем:

,

.

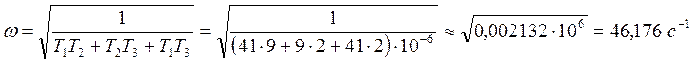Тогда из первого уравнения можно определить значение :

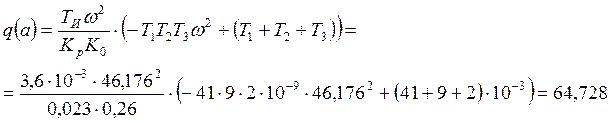
Отсюда по графику можно найти значение амплитуды:

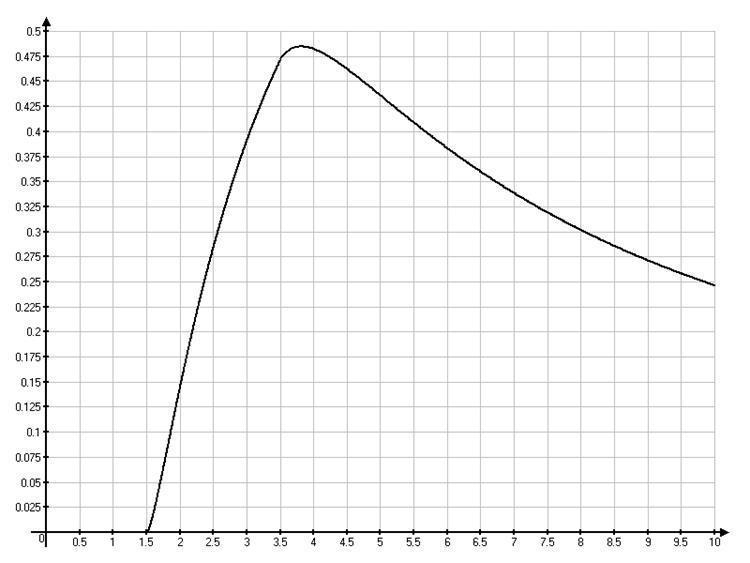
Проведем исследование системы на устойчивость решения.

Необходимо, чтобы выполнялось следующее условие:

.

В нашем случае мы получаем:

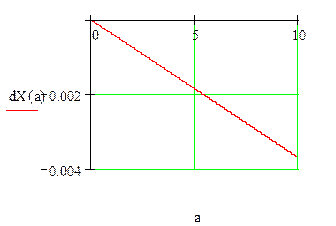
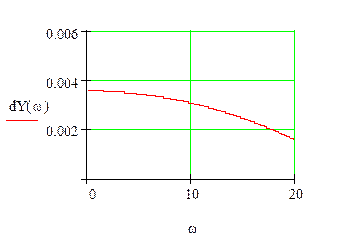
Второе слагаемое получаем равное нулю, так как .

Как видно из графиков производных первого слагаемого неравенства, произведение . Следовательно, мы получаем неустойчивое апериодическое решение, поэтому автоколебания НСАУ нельзя получить.