Динамический синтез с использованием запретных зон. Метод динамического синтеза систем автоматического управления

Динамический синтез с использованием запретных зон

 (Синтез по В.А. Бесекерскому)

Метод динамического синтеза систем автоматического управления выполняется с помощью логарифмических амплитудных характеристик. Данный метод отличается простотой и наглядностью и основан на использовании однозначной зависимости между частотными и временными характеристиками минимально-фазовых систем.

При создании автоматической системы формулируются самые разные требования, которым она должна удовлетворять. В частности, предъявляются требования к точностным и динамическим показателям проектируемой системы. Метод позволяет учесть наличие и величину возмущений, а также нестабильность ее параметров. Данные показатели определяют запретные зоны для логарифмических характеристик. В результате синтеза получается оптимальное решение, техническая реализация которого является наиболее простой. Оптимальность достигается обеспечением желаемого качества процессов в системе при минимальной полосе пропускания разомкнутой системы.

Если систему сделать полностью безинерционной, она должна иметь бесконечную мощность и, соответственно, полосу пропускания, поскольку иначе невозможно мгновенно отработать единичное ступенчатое воздействие.

Но сужение полосы пропускания ухудшает качество процессов в системе, например, повышение точности требует повышения коэффициента усиления К системы, а увеличение К расширяет полосу пропускания. Налицо - противоречие, которое гармонично решается в процессе динамического синтеза.

Метод динамического синтеза является развитием метода логарифмических амплитудных характеристик (ЛАХ). Методика синтеза включает в себя следующие этапы:

1)  построение располагаемой ЛАХ (объекта управления),

2)  построение запретных зон,

3)  построение желаемой ЛАХ системы, с учетом запретных зон,

4)  определение вида и параметров корректирующего устройства.

Построение запретных зон рассматривается ниже. Желаемая ЛАХ строится таким образом, чтобы в низкочастотной области она располагалась не ниже запретной зоны по точности. В области средних частот она должна совпадать с выбранной типовой ЛАХ. В высокочастотной области наклон желаемой ЛАХ  аналогичен наклону ЛАХ располагаемой. Сопряжение трех участков ЛАХ друг с другом выполняется исходя из практических соображений (например, простоты корректирующего устройства).

На рисунке обозначены - располагаемая передаточная функция объекта (неизменяемой части системы),    - передаточная функция корректирующего звена,            - желаемая передаточная функция разомкнутой системы. Переходя к логарифмическим характеристикам, получаем:  , откуда  . Дальнейшая реализация корректирующего устройства сводится к выбору пассивных, либо активных (на базе операционных усилителей) четырехполюсников.  Возможно проектирование параллельной коррекции, для чего выполняется соответствующий пересчет последующего корректирующего звена.

Задаче синтеза свойственна неоднозначность решения, поэтому процесс синтеза систем является повторяющимся процессом, каждая итерация которого улучшает предыдущий результат, приближая решение к оптимальному.

Построение запретных зон в низкочастотной области

Запретные зоны для логарифмических характеристик в низкочастотной области определяются в первую очередь точностными требованиями к системе.

1.  Запретная зона по точности  в системе со стабильными параметрами при ограниченном входном сигнале и отсутствии возмущений

Принято G(s) изображение g(t) оригинал.

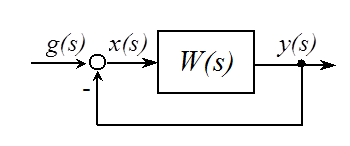
Рассмотрим систему с единичной обратной связью.  .

 .

Предварительно остановимся на нескольких частных случаях.

1.1.  Обеспечение заданной точности по входному воздействию при ограничениях

Сначала рассмотрим статический режим  .

Изображение ошибки отработки входного воздействия в статической системе, когда , равно 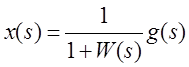. По теореме о предельных значениях  .  Тогда пр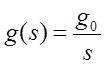и   и  .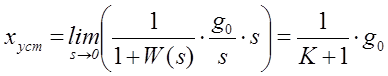

Из условия  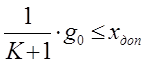 .  Данное неравенство определяет граничный коэффициент усиления системы , при котором  ошибка в системе не превышает допустимой величины. Так как обычно коэффициент усиления  К >> 1, то полученное неравенство можно привести к виду 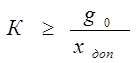, используемому в дальнейшем для построения запретной зоны.

Из передаточной функции разомкнутой системы  последовательно получаем частотные характеристики:  АФЧХ - , АЧХ  -   и ЛАХ - .  При  полученная ЛАХ асимптотически стремится к прямой   , параллельной оси абсцисс, пересекающей ось ординат в точке    .  На рисунке изображены логарифмические характеристики трех систем, каждая из которых отрабатывает постоянное входное воздействие  с ошибкой .

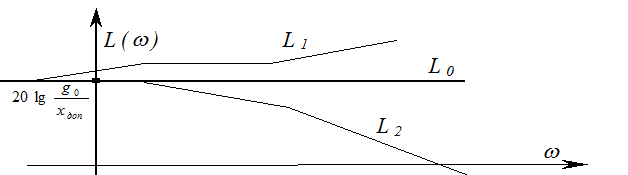
Покажем, что прямая L₀ является множеством точек, соответствующих граничному коэффициенту усиления системы, когда при отработке гармонического ограниченного сигнала  установившаяся ошибка в системе  не превосходит .  При гармоническом входном сигнале ошибка в системе также имеет синусоидальный характер. Ее установившееся максимальное значение (амплитуда) будет определяться выражением: 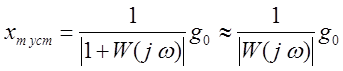, где  - коэффициент усиления системы К(ω) на частоте ω. Тогда из условия   получаем: , что подтверждает  справедливость высказанного предположения о запретной зоне по точности при отработке системой ограниченного входного сигнала:

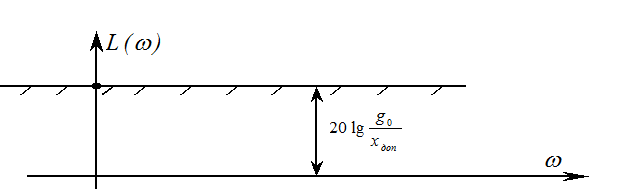
Таким образом, если необходимо, чтобы система отрабатывала ограниченный медленно меняющийся входной сигнал  с ошибкой  (), то ЛАХ синтезируемой системы в области низких частот должна проходить выше изображенной на рисунке запретной зоны.

1.2.  Обеспечение заданной точности по входному воздействию при ограничениях 

По аналогии с п. 1.1.  предварительно рассмотрим  режим    ,       ().