Погрешности преобразования информации в дискретных системах автоматического управления (ДСАУ). Примеры расчёта погрешностей преобразования информации в ДСАУ

Современные проблемы автоматизации и управления

Лекции проф. для магистров

Лекция 2. (25.09.09).

Содержание предыдущей лекции. Кратко изложена история получения погрешностей соотношений аналоговых (непрерывных) и решетчатых (импульсных) временных функций. Описаны недостатки использования соотношения Котельникова - Шеннона, обосновано преобразование Лайнвиля. Начато решение примера использования этого преобразования для оценки различия (погрешности) дискретных и аналоговых функций, которое продолжено в этой лекции.

Глава 1. Погрешности преобразования информации в дискретных системах автоматического управления (ДСАУ)

1.3. Примеры расчёта погрешностей преобразования информации в ДСАУ (продолжение решения примера 1)

          Для непрерывного интегратора, очевидно, при подстановки  в формулу (1. 13) получим:

              (1.19)

          Запишем аналогичное выражение для дискретного интегратора, при подстановки  в выражение (1. 15). Модуль  будет выглядеть следующим образом:

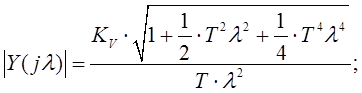                  (1.20)

Примечание составителя. (Дениса Мокринского) Полезно вспомнить, что преобразование (1.16) является частным случаем преобразования Мебиуса и называется «Билинейным». Билинейное преобразование — конформное отображение, используемое для того, чтобы преобразовать передаточную функцию K_н(s) модели линейной стационарной системы (регуляторы, фильтры) из непрерывной формы в дискретную (ДПФ) K_д(z). Оно отображает точки "" оси ординат, расположенные на "s"-плоскости, в точки окружности единичного радиуса на "z"-плоскости.      Это преобразование сохраняет устойчивость исходной непрерывной системы и существует для всех точек её передаточной функции. То есть для каждой точки передаточной функции или АФХ модели исходной системы существует подобная точка с идентичной фазой и амплитудой модели дискретной системы. Однако эта точка может быть расположена на другой частоте. Эффект сдвига частот практически незаметен при их небольших значениях, однако существенен при частотах, близких к 0,5ω_к. Интересно, что билинейное преобразование представляет собой функцию, аппроксимирующую экспоненту, которая является точным отображением "z"-плоскости на "s"-плоскость, действительно: .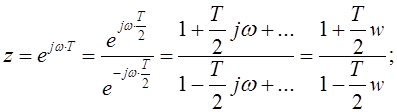

Теперь сравним  для 2-х рассматриваемых моделей. Для этого необходимо высчитать значение  на характерных частотах. В качестве первой исследуемой частоты выберем 0,5ω_к, как известно на данной частоте наблюдается наибольшее перекрытие спектра дискретного сигнала, (т. к. частоты выше 0,5ω_к являются зеркальным отображением нижних частот [Д. М.]). Для аналоговой системы получим:

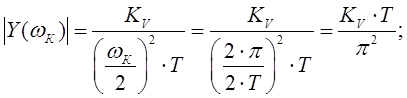           (1.21)

Для дискретной системы получим:

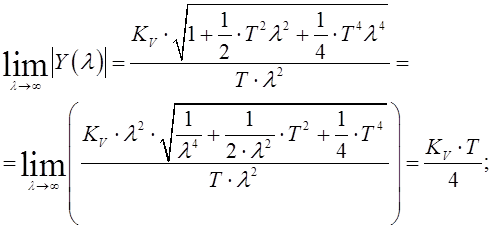                (1.22)

В качестве второго характерного значения псевдо - частоты выберем , ей будет соответствовать частота . Для аналоговой системы получим:

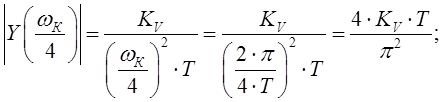               (1.23)

Для дискретной системы получим:

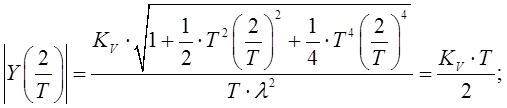              (1.24)

Определим погрешность дискретного преобразования, относительно «эталонного» аналогового:

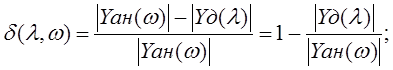             (1.25)

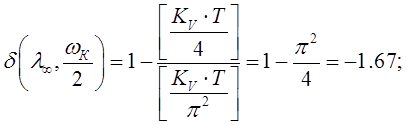           (1.26)

          Итак,  получили, что при больших частотах ошибка достигает 146%! Не стоит забывать, что большим частотам во временной области соответствует начальный участок переходного процесса.

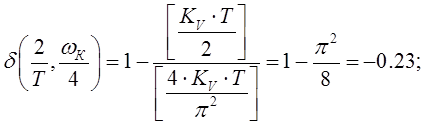                  (1.27)

Видно, что на частоте в 2 раза меньшей суммарная погрешность дискретизации и билинейного преобразования составляет –23%. Знак «–» не случаен, он говорит о том, что амплитуда спектра дискретного сигнала в каждой точке складывается из основной амплитуды спектра и из "зеркальных" его отображений (см. рис. 2. 1.)

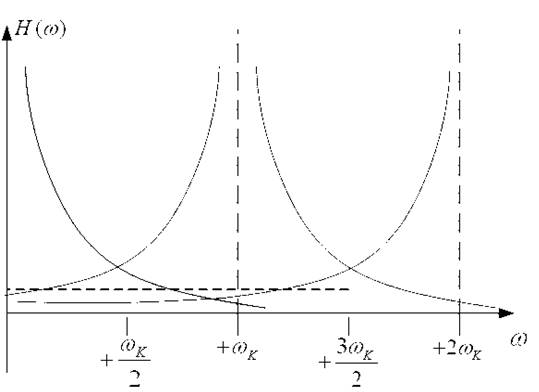
Рис. 2.1. Перекрытие составляющих спектра дискретного (импульсного) сигнала.

          Пример 2.Найдем спектры блоков дискретного интегратора "прямоугольниками с упреждением" и  интегратора "прямоугольниками с экстраполятором нулевого порядка (рис. 2. 2.)

 

Рис.2. 2. Схема блока интегратора прямоугольниками с экстраполятором

Для первой схемы имеем:

                                                                   (2.1.)

Для схемы, изображенной на рис.2. 2., получим:

                                                                       (2. 2.)

Функции (2. 1.) и (2. 2.) при переводе в плоскость "w" приобретают одинаковые значения. Поэтому

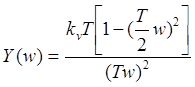,                                                       (2. 3.)

Соответственно из формулы (2. 3) найдем

                                                                             (2. 4)

В качестве второго характерного значения псевдо - частоты выберем , ей будет соответствовать частота . Для аналоговой системы получим:

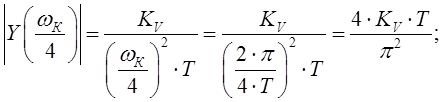                              (2. 5)

Для дискретной системы найдем:

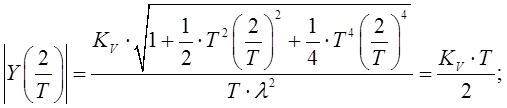              (2. 6.)

Определим погрешность дискретного преобразования, относительно «эталонного» аналогового:

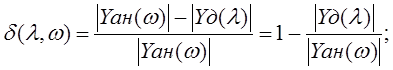             (2.7.)

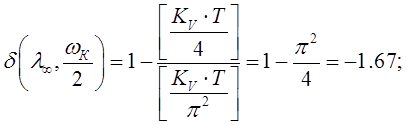           (2. 8.)

          Итак,  получили, что при больших частотах ошибка достигает 146%! Не стоит забывать, что большим частотам во временной области соответствует начальный участок переходного процесса.

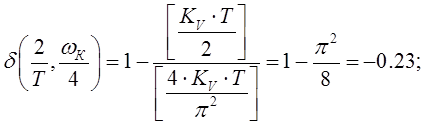                  (2. 9)

Итак, результаты вычисления погрешностей остаются прежними

          Пример 3.Найдем спектры замкнутых систем с аналоговым интегратором, с дискретным интегратором "прямоугольниками с упреждением" и с интегратором "прямоугольниками" и экстраполятором нулевого порядка.

Для аналоговой структуры получим такой выход:

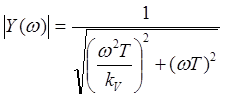
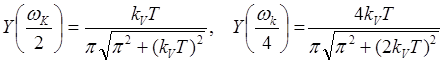                                            (2. 10)

Для первой дискретной САУ будем  иметь:

                                                                (2. 11.)

При , на основании выражения (2.11) вычислим:

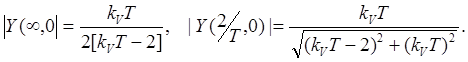
Соответственно, относительные погрешности  преобразований будут равны:

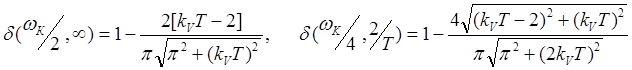        (2. 12.)

Прежде чем выполнять вычисления по формуле (2. 12) необходимо принять одно обязательное и второе желательное условия: необходимо k_VT2^*), желательно . При дальнейших расчетах принято: .

Перейдем теперь к определению выражения для  выхода второй дискретной САУ. Нетрудно убедиться, что получим вновь выражения (2.11.) и (2. 12).

Расчеты принесли таки результаты: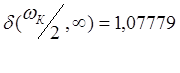

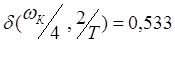
Выводы

1. На основании решения трех примеров оценки расхождений  информации в дискретных и аналоговых САУ разложением Лайнвиля (формула 1. 3.), можно установить, что методика решения таких задач имеет ряд специфических (я бы сказал малоизвестных и, практически, неизученных [С. К.])особенностей

2. Установлено, что оба метода "дискретного интегрирования" "прямоугольниками" имеют одинаковую погрешность по модулю. По-видимому, и "дифференцирование" "прямыми " и "обратными " разностями не дают различий в обработке информации.

3. Существенно различаются (численные значения) величины расхождений информации в разомкнутых (астатических) и замкнутых (статических) системах с интеграторами.

Оформил: Мокринский Д.О. 01.10.2009,скорректировала: Дзусова В.В. 25.09.2010.

____________________________________________________________________

*⁾Это условие будет пояснено в лекции 3 (С.К.)