Проблема устойчивости моделей нелинейных ДСАУ. Основные физические структуры ДСАУ и некоторые основополагающие сведения, страница 4

4. 4. Критерий абсолютной устойчивости моделей нелинейных САУ

А. Х. Гелига

Вначале  приведу "досье" на А. Х. Гелига, критерии устойчивости нелинейных ДСАУ, которого мы будем изучать.

Рассмотрим нелинейную замкнутую систему со статической нелинейностью класса 0-k (можно и k1-k2).

 

Рис.11. 7 Модель НДСА, исследуемой на абсолютную устойчивость.

Входной сигнал - . Так как мы рассматриваем состояние устойчивости системы, то принимаем ;

 - выходной сигнал;

 - статическая нелинейность;

 - некоторый дискретный сигнал, имеющий вид:

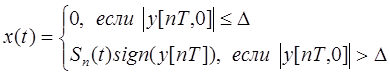                                              (3. 7)

 "порог" чувствительности входа НЭ для сигнала y[nT,0],

 - положительная аналитическая функция, которую реализует нелинейность на "n" интервале (такте).

Для функции  должны соблюдаться следующие условия:

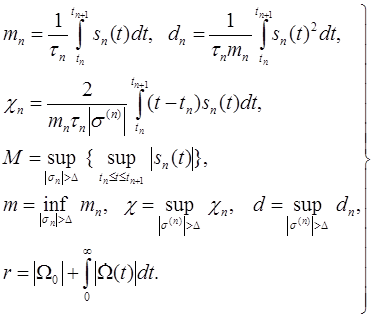                                               (4. 7)

 - порог чувствительности нелинейного элемента;

 - среднее значение функции  на " n " такте;

 - среднеквадратичное значение функции  на " n " такте;

 - коэффициент преобразования нелинейности (её коэффициент передачи),

Например, нелинейность такова, что на входе сигнал , а на выходе нелинейности , тогда её коэффициент передачи .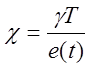

M – максимальная величина абсолютных значений импульсов сигнала .

m – минимальная величина сигнала  при условии (3. 7).

По понятиям и  их обозначениям, принятой в "Теории управления",  находится следующим образом:

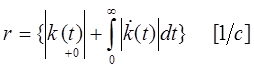,                                                         (5. 7)

где  - импульсная переходная характеристика линейной части НДСАУ.

Замечания. -Для НЭ, вырабатывающего прямоугольные импульсы, справедливо следующее:

1) =U₀ - предельное напряжение ШИП (см. рис.2. 7)

2)  – определено как: , а должно быть

Для определения  используем другую формулу в виде:

,                             (6. 7)

где -относительная продолжительность импульса на "n" такте,  - e _max (t) максимальный сигнал, который обрабатывается в этой системе.

Теорема*⁾: (А. Х. Гелига) Пусть  матрица А является "гурвицевой" (т. е. линейная часть (ЛЧ) системы устойчива в замкнутом состоянии, а в разомкнутом виде не имеет нулевых полюсов). Пусть существует число такое, что выполняется неравенство:

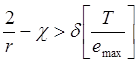,                                                                                     (7. 7),

где величины  и  определяются из выражений (6. 7) и (5. 7).

Выполняется также неравенство: такое что:

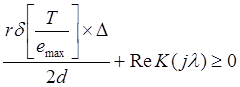,                                                                  (8. 7)

тогда модель нелинейной дискретной САУ будет устойчива абсолютно.

Следовательно, нужно найти только  и . Найдем вначале  величину δ_max Для этого заменим неравенство (7. 7) предельным равенством

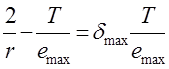                                                                               (7. 7¹)

Уравнение (5. 7) фактически определяет абсолютную величину импульсной переходной функции на входе НЭ, после идеального импульсного элемента (см. рис.11. 7.)

В нашем случае система дискретная, а уравнение (5. 7) справедливо для аналоговой системы. Предполагаем, что оно может быт использовано и в следующем виде:

                                                   (5. 7¹)

Вычислим "r" по формулам (5. 7) или (5. 7¹). При этом учтем ,что сигнал на входе НЭ (σ_n) не должен превышать e_max. Зная величину r, можно вычислить и δ_max по формуле (7. 7¹)

Теперь найдем

 и                             (9. 7)

______________________________________________________________________________________-*⁾ Нами введены изменения в теорему А. Х .Гелига, отмеченные "прямыми" скобками в выражениях (7. 7) и(8. 7). (С.К.)