Проблема устойчивости моделей нелинейных ДСАУ. Основные физические структуры ДСАУ и некоторые основополагающие сведения, страница 2

Андин предложил: , т.е. выбирать одинаковую площадь импульсов при обеих модуляциях. Следовательно, будем иметь . Отсюда можно

_______________________________________________________________________________

*⁾Ряд исследований последних лет показал, что опасно повышать частоты квантования ШИП до (10- 20) кГ. Отмечено повышение склонности обслуживающего персонала к онкологическим заболеваниям, при длительной работе с таким оборудованием.

**⁾ В нашем списке важнейших литературных работ по теории и практике ДСАУ (см. файл Лит ДСАУ _ 15а, или Лит.ДСАУ_16) упущена очень  известная и важная российская работа.: Шрейнер   Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург: Уро (Уральское отделение) РАН, 2000. - 654с.

найти эквивалентный коэффициент передачи АИМ :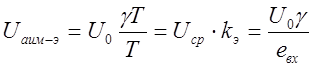, где е _вх  сигнал на входе амплитудо - импульсного модулятора (АИМ) пропорциональный γ.:

Амплитудо - импульсная модуляция линейна. Таким образом, заменили  нелинейную ШИ модуляцию линейной.

Похожий метод был разработан в СССР В.П. Шепилло [34]. Он предложил использовать "решетчатые функции средних значений", рассчитываемые на каждом интервале [nT]. Этим методом можно эквивалентировать нелинейную систему (причем любую) линейной дискретной системой с АИМ. В нашей научной школе (кафедры САУ) эти методы разрабатывали будущие доктора (DPh): австралийский ученый Хамед Мустафа (алжирец по происхождению), китайский ученый Фан - Лидзинь, российский красноярский ученый доктор техн. наук М. С. Лурье.

Резюме: оба метода: "площадей" и "решетчатых функций средних значений" – оказались очень эффективными для  аналитического исследования динамики в нелинейных ДСАУ.

В те же годы на нашей кафедре были разработаны оригинальные аналитические методы исследования динамики нелинейных дискретных систем, но сегодня они утратили актуальность.*⁾

Второе направление – возникло в те же 60-  70-х г.г. ХХ в., но было связано  с разработкой проблемы абсолютной  устойчивости нелинейных аналоговых и дискретных систем и их колебательности. Эти проблемы и задачи сохранили свою актуальность до сегодняшнего дня. Они составят главное содержание наших лекций.

Проблема исследования абсолютной устойчивости моделей нелинейных аналоговых и дискретных САУ базируется на фундаментальных принципах второго прямого метода устойчивости движений динамических систем в большом А.М. Ляпунова.

Суть метода Ляпунова – для всякой динамической системы (линейной или нелинейной) надо получить в пространстве состояний две функции: – функцию Ляпунова, описывающую движение динамической системы, и ее производную .

_________________________________________________________________________

^**) Любопытные могут заглянуть на файл "Введение 2" к курсу "Теория ДСАУ", где упомянуты имена всех разработчиков этих оригинальных методов.

В пространстве состояний есть некоторая область "G", в которой существуют эти знакоопределенные функции [V(t)>0 и  W(t)<0].

При  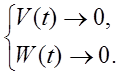 Это достаточное условие асимптотической устойчивости динамической системы в большом.

Необходимо было сделать два доопределения:

1. Пусть заменяем непрерывные V(t) и  W(t) функции дискретными, т.е. рассматриваем решетчатые несмещенные функции V[nT] и  W[nT]. Тогда эти несмещенные функции не выходят за границы области G. Но где гарантия, что смещенные функции будут лежать в области G? Необходимо доопределить, что смещенные функции находятся в области допустимых значений:

.