2. Доопределение связанно с понятием абсолютной устойчивости. Для любых нелинейных систем, нелинейности которых принадлежат по А.И. Лурье к классам "0-k" или "k1-k2", необходимо было найти доказательство, что область G может быть расширена до бесконечности. Потому, как понятие "абсолютной устойчивости" предполагает, устойчивость движений динамической системы "в целом", а не "в большом".
Эти два доопределения были сделаны советскими учеными Е.А. Барбашиным и Н.Н. Красовским (теорема Барбашина - Красовского)*)
Колебательность [50] - это свойство нелинейных систем иметь орбитальную устойчивость установившихся движений. К таким движениям принадлежат и автоколебания. Эту проблему в наших лекциях не будем затрагивать.
4. 2. Модели нелинейных ДСАУ
С позиций исследования устойчивости можно выделить четыре основных модели нелинейных ДСАУ
I. Рисунок 4. 7.
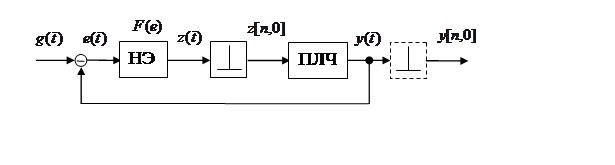
Рис.4. 7. Модель нелинейной ДСАУ со статической нелинйностью в аналоговой части и линейным экстраполятором.
Здесь ПЛЧ – приведенная
линейная часть ДСАУ. Её передаточная функция: ![]()
II. Рисунок 5. 7.
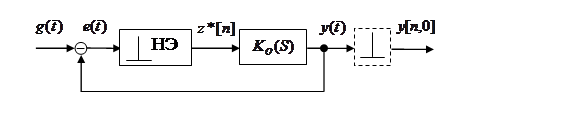
Рис. 5. 7. Модель нелинейной ДСАУ с нелинейным экстраполятором, включающим идеальный импульсный элемент (квантователь) и различные виды нелинейностей.
Здесь - НЭ – нелинейный экстраполятор (например, ШИМ - I).
В отличие от модели I на
вход ![]() приходит некоторая непрерывная
функция.
приходит некоторая непрерывная
функция.
_____________________________________________________________________________________________________________________________
*)Этих источникв нет в наших списках литературы.
Барбашин Е. А. Функция Ляпунова. -М.: Наука, 1970.
Красовский Н. Н. Некоторые задачи теории устойчивости движения.- М.: Физматгиз, 1959.
Например:
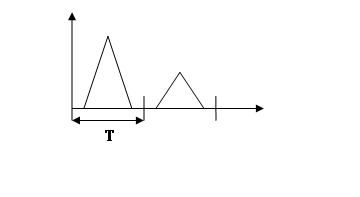
Рис. 6. 7. Сигнал Z*[nT] на выходе нелинейного экстраполятора НЭ.
В данном случае могу возникнуть совершенно другие решения проблемы устойчивости, чем в модели I.
III. Рисунок 7. 7.
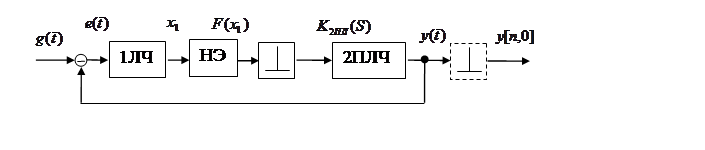
Рис. 7. 7. Модель нелинейной ДСАУ со статической нелинйностью в разделенной аналоговой частью и линейным экстраполятором
По сути это нелинейная
аналого - дискретно- - аналоговая САУ (НАДАСАУ).Здесь: НЭ – статический
нелинейный элемент; 2ПЛС – вторая приведенная линейная часть системы и её ПФ ![]()
IV. Рисунок 8. 7.
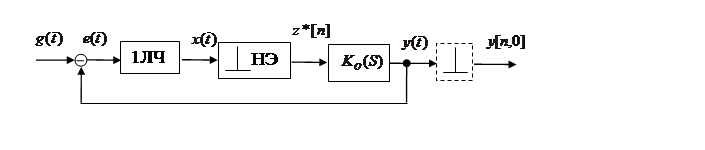
Рис. 8. 7. Модель нелинейной ДСАУ с нелинейным экстраполятором и разделенной аналоговой частью
Могут быть и другие структуры НДСАУ, но мы их не приводим из следующего соображения. При оценке устойчивости модели исследуется автономная система без воздействия внешних сигналов, тогда модели I-III и II-IV становятся однотипными, ( как и возможные другие модели). Поэтому в дальнейшем будем рассматривать только модели I и II.
4.3. Критерий абсолютной устойчивости нелинейных ДСАУ
Я. З. Цыпкина
Яков Цыпкин предложил для структур I типа исследовать устойчивость с помощью следующего критерия:
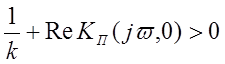 (1.7)
(1.7)
1. В этом случае ![]() - есть статическая
нечетно-симметричная нелинейность, принадлежащая классу 0-k. Это означает, что она имеет вид
рис.9. 7
- есть статическая
нечетно-симметричная нелинейность, принадлежащая классу 0-k. Это означает, что она имеет вид
рис.9. 7
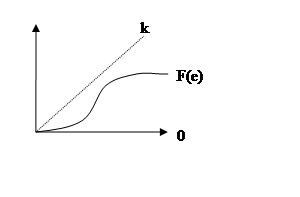
Рис.9. 7.Вид нелинейности F(e) (по А. Лурье)
2. ![]() - передаточная функция (ПФ)
модели приведенной линейной части ДСАУ, которая является устойчивой в замкнутом
состоянии. Кроме того, эта ПФ не имеет нулевых полюсов. Относительная угловая
скорость
- передаточная функция (ПФ)
модели приведенной линейной части ДСАУ, которая является устойчивой в замкнутом
состоянии. Кроме того, эта ПФ не имеет нулевых полюсов. Относительная угловая
скорость ![]() .
.
Иначе говоря, рассматривается такая система:
![]() ,
где
,
где ![]() , то есть рассматриваются только
статические системы.
, то есть рассматриваются только
статические системы. 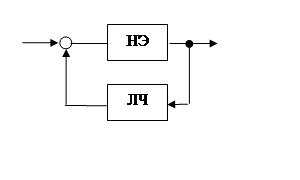
Рис. 10. 7Модель НДСА, исследуемой на устойчивость
Пример.  ,
,
Полином знаменателя
замкнутой линейной системы ![]() должен содержать только левые корни. Матрица должна быть гурвицевой.
должен содержать только левые корни. Матрица должна быть гурвицевой.
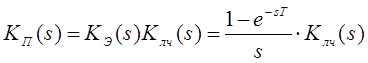 ,
, ![]()
![]() (2.
7)
(2.
7)
Замечания:
1) Процедура расчета характеристик по формуле (2. 7) очень сложна.
2) Формулу (1. 7) можно применять в том случае, если модуляция в системе амплитудно-импульсная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.