









Синтез модального управления
Из классической теории САУ известно, что динамику системы автоматического управления можно сделать любой, наперед заданной. (Вспомним корректирующие устройства последовательного, параллельного, комбинированного типов, метод ЛАХ ‑ как метод синтеза корректирующего устройства).
Можно ли сделать это при представлении модели системы в уравнениях переменных состояния?
Теорема.
Необходимое и достаточное условие полной управляемости линейной стационарной
системы ![]() и заключается в том, чтобы
матрица управляемости Р = [ В | АВ |…|
и заключается в том, чтобы
матрица управляемости Р = [ В | АВ |…|![]() Аn-1В
] имела бы ранг n,
то есть пара (А,В) –
управляема.
Аn-1В
] имела бы ранг n,
то есть пара (А,В) –
управляема.
Под управляемостью понимают существование управления u(t), достаточного для перевода системы за конечное время tк – to из состояния xo в xк, где xo и xк – две произвольные точки пространства состояний размерности n.
Постановка задачи модального управления
Замкнутая система автоматического управления должна иметь динамику, заданную эталонной моделью j(s) = sn + gn-1sn-1 +…+ go. (1)
Эталонная модель (коэффициенты характеристического уравнения системы) выбирается исходя из требуемых показателей качества (tn - время переходного процесса, s - перерегулирование, статическая и динамическая точности).
Другими словами: требуется обеспечить заданное расположение полюсов передаточной функции системы (моды – полюса).
Синтез осуществляется в два этапа.
1. Выбор расположения полюсов, имеющего целью удовлетворить заданным техническим требованиям (определение требуемых коэффициентов уравнения (1) системы).
2. Проектирование регулятора, обеспечивающего желаемое расположение полюсов.
2.1. Приведение математической модели объекта к нормальной форме, когда вектор состояния – вектор фазовых переменных.
2.2. Нахождение регулятора применительно к этому виду описания.
2.3. Преобразование регулятора к первоначальной форме математической модели.
Все этапы синтеза выполняются с помощью ЭВМ.
Пусть имеется объект ![]() ; (2)
; (2)
Существует неособенное преобразование координат x = Mz, (3)
приводящее
систему (2) к нормальной форме ![]() , (4)
, (4)
где матрицы Aк и Bк имеют вид:
Aк
= ![]()
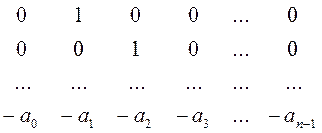
![]() ;
Bк =
;
Bк = ![]() ;
;
(2) с учетом (3) Þ ![]() Þ
Þ ![]() .
.
Тогда в (4) ![]() ,
, ![]() .
.
Пусть регулятор ищется в виде u
= g - Kкzили с учетом (2) (в исходных
переменных) ![]() ,
, ![]() . (5)
. (5)
Тогда замкнутая система имеет вид
|
|
Þ |
(6) |
Получим характеристическое уравнение матрицы Ак - ВкKк:
Если Kк =
(k1 ,
k2 ,…,
kn), то
ВкKк =
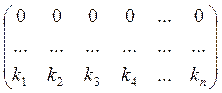 ;
;
Ак - ВкKк = 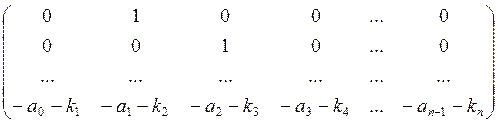 ;
;
Тогда det(sE - (Ак - ВкKк)) = sn + (an-1 + kn) sn-1 + … + (a0 + k1) = 0; (7)
Сравнивая желаемый характеристический полином (1) с характеристическим полиномом замкнутой системы (7) можно, приравнивая коэффициенты при одинаковых ступенях S, получить:
|
gn-1 = an-1 + kn, gn-2 = an-2 + kn-1, откуда: … g0 = a0 + k1, |
k1 = g0 - a0, k2 = g1 - a1, (8) … kn =gn-1 - an-1. |
Таким образом для системы ![]() найдена
матрица обратной связи Kк (8)
по желаемому характеристическому уравнению синтезированной системы и характеристическому
уравнению матрицы Ак объекта управления.
найдена
матрица обратной связи Kк (8)
по желаемому характеристическому уравнению синтезированной системы и характеристическому
уравнению матрицы Ак объекта управления.
Тогда требуемая динамика (1) объекта управления, представленного уравнением (2), будет достигнута, если регулятор u = g - Kx будет определяться матрицей K = KкM-1, полученной после обратного преобразования координат (3).
Переход от математической
модели вида (2) к нормальной форме (4) обычно выполняется без проблем.
Например, сначала из (2) можно получить уравнение вход-выход системы в
операторной форме, а затем уже перейти к системе уравнений в нормальной форме
(в фазовых координатах). Прямой способ перехода от (2) к (4) выполняется чуть
сложнее. Сначала составляется матрица управляемости Р = [ В | АВ |…|![]() Аn-1В
], затем находится ее обратная: Р-1,
далее вычисляется матрица Ак
= Р -1 *A*Р.
Аn-1В
], затем находится ее обратная: Р-1,
далее вычисляется матрица Ак
= Р -1 *A*Р.
Для нахождения матрицы М
обратного преобразования координат (3) сначала следует составить матрицу Рk= [ Вk |
AkВk |…|![]() ( Ak)n-1 Вk],
( Ak)n-1 Вk],
После чего находится М-1= Рk*Р-1, обратив которую можно получить и М.
Если процедура вычисления матрицы М вызывает проблемы, то для нахождения матрицы К регулятора можно воспользоваться формулой Аккермана:
![]() . (9)
. (9)
Способы задания характеристического полинома эталонной модели
Основные требования к эталонной модели задаются показателями: tn - время переходного процесса, s - перерегулирование, статическая и динамическая точности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.