Синтез модального управления. Постановка задачи модального управления. Эталонная модель (коэффициенты характеристического уравнения системы), страница 3

Полученная система имеет решение, если ранг матрицы 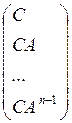  равен n!

Что и требовалось доказать.

Данная теорема дает один способ определения вектора состояния (по y и его производным и u и ее производным).

Наблюдатель (фильтр) Люенбергера

Наблюдатель -  это динамическая модель, описываемая уравнением:

_н = А₁х_н  + В₁u+ В₂y.

Замечания:

1)  Объект наблюдаемый. (Пара (А, С) – наблюдаема).

2)  Наблюдатель – модель объекта, т.е. если x(t₀) = x_н(t₀), то модель наблюдателя должна быть           _н = Ах_н  + Вu.

Если     x_н(t₀) ¹ x(t₀),   то     x_н(t) ® x(t),  при     t ® ¥.

Следовательно, можно наблюдатель представить в виде:

_н = Ах_н  + Вu + K_н(Cx_н - y_н),

где выбор матрицы К_н определяется скоростью сходимости x_н(t) ® x(t)

	u

 

uU

Модель наблюдателя – модель объекта с дополнительной обратной связью.

Для определения параметров этой обратной связи вычтем уравнение объекта из уравнения наблюдателя.

_н - = А(х_н  - x) + K_нC(x_н - x) = (A - K_нC) (х - x_н)

Получили динамическую модель  = (A -K_нC),   (х - x_н),  собственное движение которой определяется собственными числами матрицы A - K_нC. И если пара (А, С) – наблюдаема, то из ТАУ следует, что можно подобрать такую K_н, что задача будет решена при требуемом качестве.

Например, при желаемом апериодическом движении системы  = (A -K_нC)   (экспоненциальный закон) можно подобрать соответствующие значения коэффициентов обратной связи наблюдателя K_н по аналогии с синтезом модального управления. При этом полоса пропускания w_0н наблюдателя должна соотноситься с частотой среза w₀ собственно системы управления как

w_0н = Qw₀,    Q = 3 ¸ 10.

Меньше – нежелательно, потому что переходный процесс относительного движения должен быть более быстрым по сравнению с процессами в объекте управления.

А Q > 10 - нельзя, так как наблюдатель будет чувствителен к шумам.

Рассмотрим систему

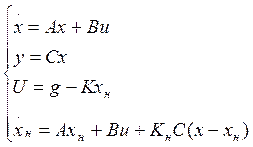              или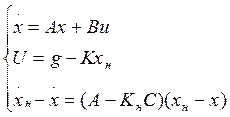        

Если ввести обозначения x_о = x_н – x,      x_н = x₀ + x, тогда рассматриваемая система примет вид

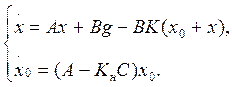
Динамика этой системы определяется матрицей

 = ;

Наблюдатель не влияет на динамику системы управления (объект управления - регулятор), а лишь добавляет в это движение свои собственные числа,

т.к. det(Es – ) = det(Es – A + BK) * det(Es – A + K_нС).

Редуцированный наблюдатель Люенбергера

(наблюдатель пониженной размерности)

Пусть вектор выхода yÎ ;  вводится дополнительный вектор  zÎ ;  размерность которого такова, что   q + p = n.

Тогда  вектор состояния x_н наблюдателя может быть определен как 

x_н = С₂y + С₁z,       С₂ Î ,       С₁ Î , а наблюдатель будет иметь модель    = А_нz + В₂u + В₁y.

Компоненты вектора  y  - линейно независимы. Требуется выбрать матрицы А_н, В₁, В₂, С₁, С₂, такие, что:

1)  x_н(t)® x(t) по экспоненциальному закону;

2)  x_н  являлось бы линейной комбинацией  yи zв момент времени  t.

Условие 2) определяется выбором матриц  С₁  и  С₂. Условие 1) выполняется тогда и только тогда, когда:

a)  матрица А_н - устойчивая (отрицательно определенная),

b)  Существует (n – p) n матрица  П, такая, что  ПА – А_нП = В₁С,

c)  ПB = В₂,

d)  матрица (С₁ С₂) удовлетворяет условию   = E_n.

Покажем, что так должно быть.

Вводим вектор e = z – Пxz = e + Пx.

Тогда   = П +   =  А_нz + В₁y + В₂u,

или с учетом уравнения объекта

ПAx + ПBu +  = А_нz + В₁Cx + В₂u,      а с учетом z = e + Пx получаем

ПAx + ПBu +  = А_нПx + А_нE + В₁Cx + В₂u,

или (ПАx - А_нП - В₁C)x + (ПB - В₂)u +  - А_нe = 0.

Отсюда получаем условия совместимости:

 = А_нe,    ПАx - А_нП = В₁C,   ПB = В_2.

Итак:   Линейная связь между векторами  x  и  z существует, если уравнение ПАx - А_нП = В₁C  имеет решение при произвольном выборе матрицы В₁, что возможно, если матрицы A и А_н не имеют одинаковых собственных чисел.

Начальные условия удовлетворяют соотношению:

z_о = Пx_о       (что не всегда бывает, но наступает с течением времени)

Кстати,  решение уравнения  = А_нe  имеет вид:

e(t) = z(t) – Пx(t) = exp(А_н(t – t₀))*( z₀ - Пx₀).

Кроме того x_н = С₁z + С₂y (так определено в начале), а с учетом z = Пx + e

x_н = С₁Пx + С₂Cx + С₁e.

Тогда, учитывая, что e(t) = exp(А_н(t – t₀))*( z₀ - Пx₀), x_н =  x + С₁e,   имеем  x_н =  x + e 

где e = C₁ = C₁.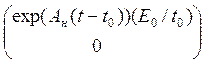

А так как  e® 0,  то x_н = (С₁П + С₂C)x,      то есть  = E.

Тогда, если rang = n,   то   rang = n.

и если rangC = p, то rang П = n - g  (число линейно-независимых  строк П).