Методы линеаризации нелинейностей и нелинейных систем. Линеаризация касательными. Статистическая линеаризация статических и динамических нелинейностей, страница 6

Для динамической нелинейности запись комплексного коэффициента передачи:    (как и ранее, получается при замене  в выражении .

Структура гармонически линеаризованных нелинейных систем

Если в НСАУ включена двузначная или динамическая нелинейность, то модель системы можно представить в виде, изображенном на рисунке:

Линеаризованная нелинейность представлена  форсирующим звеном, операторный коэффициент передачи которого: . Такое звено повышает устойчивость линейных САУ. Можно предположить, что если ввести в НСАУ нелинейность с гистерезисом, то устойчивость системы будет лучше (только гистерезис должен быть опережающим).

Если нелинейность в системе статическая однозначная, то в структурной схеме она будет заменена пропорциональным звеном:

Автоколебания в нелинейной системе

В реальной линейной системе автоматического управления невозможны колебания постоянной амплитуды без наличия специального периодического входного воздействия. Собственные движения могут иметь незатухающий вид только в том случае, если характеристическое уравнение ЛСАУ имеет хотя бы один чисто мнимый корень (с нулевой вещественной частью).

В НСАУ могут существовать особые режимы «автоколебаний». Автоколебания – собственные колебания в нелинейной системе, обладающие свойством устойчивости, то есть способностью сохранять амплитуду и форму (частоту) колебаний. Автоколебания в реальных системах появляются из-за наличия гистерезиса, люфта, всевозможных зазоров в механических соединениях, наличия реле и других причин. Автоколебания в таких нелинейных системах ухудшают качество переходного процесса, не дают ему окончательно затухнуть. В особо точных системах позиционирования автоколебания просто недопустимы.

Для расчета такого рода колебаний подходит метод гармонической линеаризации, который позволяет определить амплитуду и частоту первой гармоники этих колебаний.  

После линеаризации нелинейного элемента данным методом рассматривают следующую структурную схему:

Расчет выполняется с использованием критериев устойчивости линейных систем. Например, согласно критерию Найквиста система находится на границе устойчивости (то есть в ней возможны незатухающие и ненарастающие колебания) когда годограф АФЧХ разомкнутой САУ проходит через точку с координатами  (-1, j0): 

, где   и - амплитуда и частота возможных автоколебаний. Данное равенство сводится к уравнению:

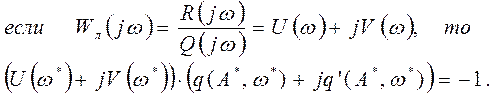
Выделим в полученном линейную и мнимую части:

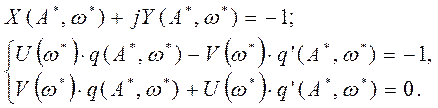
Решением этой системы являются  искомые  и . 

Данная задача может быть решена и графически. Для этого уравнение  преобразуется к виду: 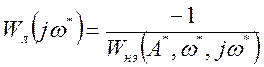 . В случае статических нелинейностей  .

Как следует из рисунка, строятся две кривые:  и . По точке их пересечения В определяется  из уравнения кривой  и  из кривой  .

Решение данной задачи может быть найдено и на плоскости логарифмических характеристик (кому как удобнее).

Следует иметь ввиду, что решений может быть несколько, кроме того,  и  могут вовсе не быть истинными параметрами автоколебаний, так как метод гармонической линеаризации дает лишь необходимое условие наличия автоколебаний. Достаточное условие должно заключать в себе рассмотрение всех гармоник, что практически нереально.

В том случае, если в результате решения не найдено искомых  и , можно с уверенность сказать, что в системе отсутствуют автоколебания.

С помощью метода гармонической линеаризации могут быть решены следующие задачи:

Задача №1. Оценка дихотомии НСАУ, то есть оценка структуры НСАУ, в которой не может быть автоколебаний.

Задача №2. Оценка симметричных и несимметричных автоколебаний в НСАУ, расчет их заданных параметров и устойчивость.

Задача №3. Оценка устойчивости динамических процессов в НСАУ. Речь идет о процессах, вызванных внешними возмущениями типа 1(t).

Задача №4. Расчет динамических процессов в НСАУ и определение их качества (анализ НСАУ).

Задача №5. Синтез НСАУ. Разработано много методов синтеза различных классов НСАУ. Есть метод динамического синтеза НСАУ, разработанный  И.П. Пальтовым.