Методы линеаризации нелинейностей и нелинейных систем. Линеаризация касательными. Статистическая линеаризация статических и динамических нелинейностей, страница 3

Все постоянные времени знаменателя здесь положительны, поэтому ЛЧ устойчива в разомкнутом состоянии. Запишем теперь передаточную функцию (ПФ) линейного прототипа этой НСАУ в разомкнутом состоянии:

. В числителе, естественно, появилось значение коэффициента передачи безинерционного звена "k", предельное значение которого "k_kr" необходимо определить.

Найдем по критерию Гурвица условия устойчивости прототипа. Полином знаменателя D(s) замкнутой ЛСАУ будет иметь такой вид:

, или

.

Составим определитель Гурвица:      .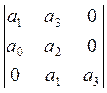

Отсюда имеем: 0,65х1,6 - 0,05 - 0,05 х k_kr = 0.    k_kr =19,8.

Теперь проверим соблюдение неравенства . Очевидно, если , то неравенство соблюдается, и нелинейность F(e) лежит внутри заданных секторов. НСАУ устойчива "в малом".

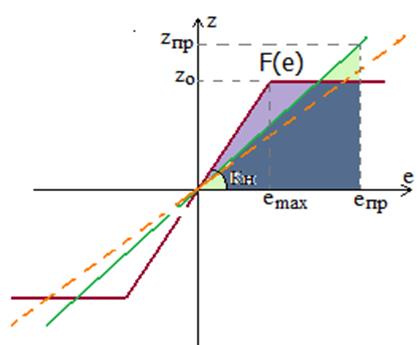
Если же , т. е. "горб" нелинейности (см. рис..) "выпирает" из заданного сектора, то НСАУ с такой НЧ и ЛЧ неустойчива даже "в малом." Что же можно предпринять? Очевидно, если возможно, изменить нелинейность, уменьшая z _o  или увеличивая e_max. Если такие простые меры не помогли, то дальнейшее использование такой НСАУ проблематично!

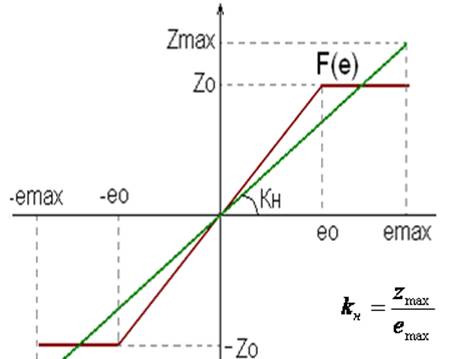
Выполним линеаризацию статической, нечетно-симметричной, кусочно-линейной, однозначной нелинейности методом секущей:

В качестве условия линеаризации применяют формулу, предложенную в первой гипотезе  М. Айзерманом: 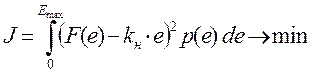 , где p(e) - плотность распределения вероятности случайного входного сигнала.

Задача отыскания  k_н  является экстремальной задачей. Ее решение можно найти из условия: . В случае детерминированного характера сигнала e(t) полагается  p(e)=1.  

Тогда после дифференцирования интеграла на отрезке от  -Е_max до Е_max  получаем: 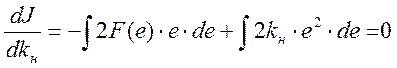,    откуда   .  

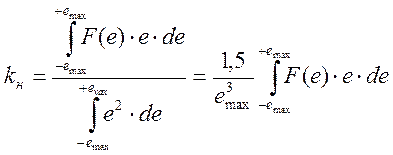Нетрудно убедиться, что вторая производная от Jположительна. Поэтому полученное значение k_нмаксимально.

Для нелинейности, изображенной на рисунке, получаем:

.

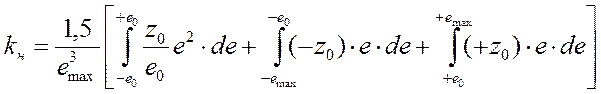После упрощения получаем:

.

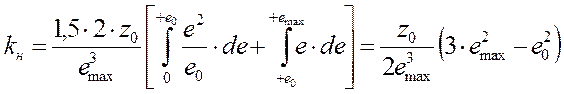В случае двузначных нелинейностей по предложению П.А. Нечаева гипотезы М. Айзермана претерпели изменение. В этом случае экстремальная задача  отыскания коэффициента линеаризации  сведена к форме:

Затем обходится нисходящая ветвь (от + е_max  до - е_max).

Для определения оптимального значения k_н интегрирование  по  контуру заменяется двумя линейными интегралами такого вида:

 

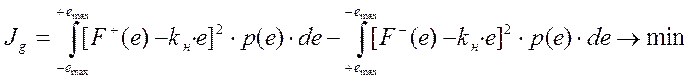
Далее задача решается тем же методом, как и ранее.

Гармоническая линеаризация нелинейностей и нелинейных  систем

Основы метода гармонической линеаризации

Основы метода разработаны в Советском Союзе в 30-е годы 20 века (1932 - 1937гг.) математиками - академиками Николаем Митрофановичем Крыловым и Николаем Николаевичем Боголюбовым, "как новые методы нелинейной механики". В своё время метод получил название «метод гармонического баланса».  Позднее, (1941 - 1947гг.) Лев Семенович Гольдфарб предложил его использовать для анализа нелинейных САУ. Только в 50 - е годы  в научных публикациях крупнейших зарубежных специалистов (H.Chestnut, R. W. Mauer и др.) Англии, (K. Magnus, W. Oppellt и др.) Германии,(R.J. Kochenburger, N.B. Nichols и др.) США, появились разработки этой проблемы. Наибольший вклад в разработку проблемы внесли российские ученые чл. корр. АН СССР Евгений Павлович Попов и профессор Иван Петрович Пальтов.

Метод гармонической   линеаризации предназначен для представления нелинейной части системы линейным звеном, если сигналы в системе могут рассматриваться как гармоническими. Этот метод эффективно используется для исследования периодических колебаний в автоматических системах, в том числе для определения условий отсутствия этих колебаний, как вредных.

Метод является приближенным и применяется, когда линейная часть системы устойчива или нейтральна и описывается дифференциальным уравнением любого порядка, а нелинейный элемент может быть как однозначным, так и многозначным. Кроме того, ЛЧ является фильтром низких частот, то есть отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники.