Сущность метода сводится к следующему. Нелинейный элемент системы заменяется линейным звеном, параметры которого определяются при гармоническом входном воздействии из условия равенства амплитуд первых гармоник на выходе нелинейного элемента и эквивалентного ему линейного звена (при условии возникновения в замкнутой системе незатухающих колебаний).
После прохождения гармонического сигнала через нелинейный элемент (при отбрасывании старших гармоник) получают:
.
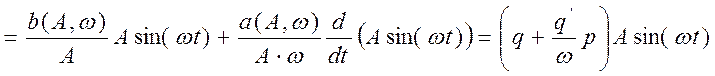Таким образом, гармонический сигнал, проходя через нелинейный элемент, домножается на некоторое операторное выражение, которое естественным образом называется эквивалентной операторной функцией НЭ:
.
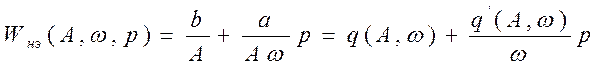Исходя из существования незатухающих автоколебаний формулируются условия эквивалентности (однозначности) протекания периодического процесса в разомкнутой и замкнутой системах. (Условия эквивалентности гармонического баланса).
1. Гармонический сигнал действует внутри системы, то есть он не приходит извне и не является управляющим.
2. Линейная часть системы либо статически устойчива, либо нейтральна, то есть в ней не должно быть не минимально-фазных звеньев.
Интерпретировать эти положения можно следующим образом.
Пусть
имеется разомкнутая система с задающим сигналом вида 
:
Тогда
выходной сигнал в разомкнутой системы будет равен: 
.
Замкнем нелинейную систему.
Для того,
чтобы в замкнутой системе возникли незатухающие колебания, необходимо выполнение
следующих условий: при 
сигналы x(t) и y(t) в разомкнутой
и замкнутой системах должны быть равны по модулю, но иметь противоположные
знаки.
Иными словами,
должно выполняться 
и 
.
Два "простеньких"
уравнения гармонического баланса имеют существенный физический смысл. Во-первых,
входной сигнал x(t) гармонически
линеаризуемой НСАУ должен быть противоположен по фазе сигналу
выхода y(t). Во вторых, и 
и 
, но должны быть равны по
модулю 
. Иначе гармоническая линеаризация
в данной НСАУ невозможна.
Гипотеза Фильтра
В общем случае при гармонической линеаризации автономных замкнутых систем на выходе нелинейного элемента появляется полигармоническая функция z(t). Полигармонический сигнал z(t) можно разложить в ряд Фурье. Следовательно, появляются гармоники 2ω, 3ω, 4ω…и т. д. Сигнал y(t) тоже будет иметь много гармоник.
Очевидно, четно-симметричные нелинейности (ЧСН) будут воспроизводить четные гармоники, а нечетно - симметричные нелинейности (НСН) воспроизводят нечетные гармоники. Это следует учитывать в дальнейших исследованиях.
Наличие высших гармоник в сигнале z(t) затрудняет
выполнение условий эквивалентности гармонического баланса. Ослабление их
влияния на выходную
координату y(t) достигается
при определенных параметрах линейной части НСАУ. Решение этой задачи в теории
НСАУ получило название "гипотеза фильтра", определяемое
неравенством: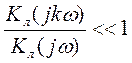 
.
Требование гипотезы сводится к тому, чтобы дополнительные гармоники, оставшиеся в выходном сигнале y(t) были много меньше (по модулю) первой гармоники. Следовательно, желательно иметь амплитудно-частотную характеристику линейной части исследуемой (проектируемой) нелинейной САУ [Α(ω)] следующего вида:
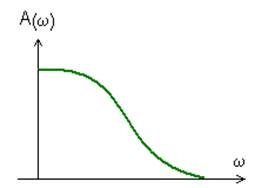
Полученное неравенство еще более упрощается при использовании логарифмических частотных характеристик для ЛЧ.
При 
- 20дб/дек
для (ЧСН)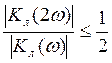 
для (НСН) 
.
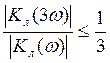При - 40дб/дек
для (ЧСН)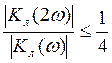 
для (НСН) 
.
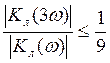Если решаются задачи управления НСАУ, и
сигнал 
имеет заданный диапазон
изменения 
, то вышеуказанные соотношения
проверяются
во всем заданном диапазоне изменения частот.
В
случае необходимости проверки условия существования автоколебаний с
частотой 
достаточно проверить гипотезу
только при этой частоте.
Комплексный коэффициент передачи статического нелинейного звена
Рассмотрим типовую нелинейную систему первого класса.
При наличии в системе
автоколебаний сигнал рассогласования x1(t) будет иметь вид: 
, где 
.
На выходе НЭ имеем реакцию x2(t) = z(t) периодическую полигармоническую функцию, которая раскладывается в ряд Фурье.
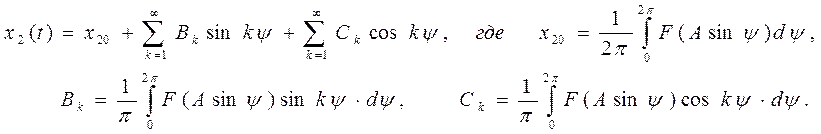
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.