Методы линеаризации нелинейностей и нелинейных систем. Линеаризация касательными. Статистическая линеаризация статических и динамических нелинейностей, страница 2

Попытаемся внести предельную ясность в этот важный вопрос.

Через «рабочую точку», как показано на рис., проведена касательная , где k_н – коэффициент линеаризации нелинейности.

Поскольку F(e) = z, то , где  - добавка нелинейной функции z при изменении аргумента  е  на величину .

Разложим F(e) в ряд Тейлора при  :

Обычно, поясняя этот метод линеаризации, говорят: "будем рассматривать первые два члена ряда Тейлора".

Следовательно, можно считать, что  при малых значениях .

Тогда рассматриваемую нелинейную структуру можно заменить линейной при  :

Анализ и синтез исследуемой НСАУ теперь можно приближенно выполнить по методикам, пригодным для ЛСАУ.

На самом деле  и  различны, поскольку имеются третий и последующие члены ряда Тейлора, которые математически точно определяют эту погрешность .

Попытаемся оценить эти отличия. Итак, запишем вновь разложение F(e) в ряд Тэйлора:

 , откуда

… ,

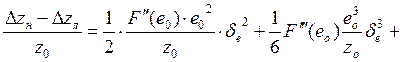Для выпуклых кривых <0, но и , а для вогнутых кривых обе эти зависимости положительны. Кроме того, учтем, что обычно третья производная численно меньше второй и числено резко уменьшается с возрастанием "п". Например, при очень большой величине =0,2, =0,04, уже очень малая =0.0016. Поэтому последнее выражение можно обоснованно  заменить следующим приближенным равенством:

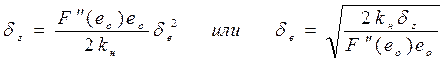, где  и - относительные изменения входной и выходной координат статической нелинейности, определенные относительно базовых параметров рабочей точки .

Пользоваться полученным выражением очень просто, задаемся величиной  и вычисляем конкретную величину . Вот суть этих длительных пояснений.

Пример: Задана однозначная четно-симметричная нелинейность:

.	Выбираем на ней рабочую точку с координатой eo =3, тогда zo =39. Вычислим производные Теперь эти значения подставим в выражение и найдем:  при , а при !!! Так что говорить о "малости" приращения аргумента Δe нельзя.

В заключение напомним, что при такой линеаризации НСАУ структура эквивалентной линейной САУ должна иметь два сигнала управления. Первый, постоянный сигнал g_o необходим для вывода системы в рабочую точку с координатами z_o  и  e_o.  Величина сигнала g_o вычисляется в соответствии с формулой 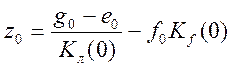, а переменный сигнал воспроизводит приращения ,  и .

 

Линеаризация секущими

Данный способ применяется когда  необходимо линеаризовать нелинейность при больших отклонениях входного сигнала e или при "многоступенчатости" однозначной  статической характеристике нелинейного элемента. Например, такие нелинейности присущи всем "аналого-цифровым" и "цифро-аналоговым" преобразователям (АЦП и ЦАП) любых вычислительных машин. Метод основан на двух гипотезах М. А Айзермана.

Гипотеза 1. 1.1. Пусть имеется нелинейная САУ с устойчивой линейной частью K_o(p) и произвольная аналитически заданная однозначная статическая нелинейность.

1. 2. Нелинейность можно заменить линейным эквивалентом с коэффициентом передачи 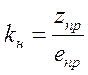 ,  который находится как решение экстремальной задачи: 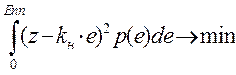, где  p(e) - плотность распределения вероятности входного сигнала, если он является случайной величиной.

При расчетах нужно принять p(e)=1, так как сигнал e(t) детерминированный. Устремлять интеграл к нулю нельзя, это приводит к комплексным корням для значения k_н, хотя реально данный коэффициент - вещественная положительная величина.

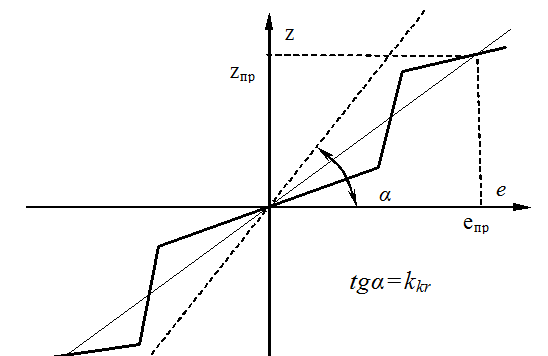
Гипотеза 2. Для оценки устойчивости исходной нелинейной системы её  можно заменить линейным прототипом с такой же ЛЧ, но вместо нелинейной части F(e) - линейное безинерционное звено с коэффициентом передачи k_н.

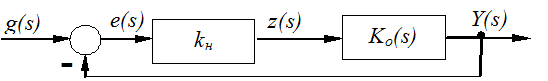
Тогда устойчивость НСАУ "в малом" будет такой же, как и для ЛСАУ, если нелинейность F(e) располагается внутри заданных секторов (между прямыми " k_н e" и "k_kr e"), то есть соблюдается следующее условие:

, где k_{kr -}предельный (наибольший) коэффициент передачи ЛСАУ, выводящий её на границу устойчивости.

Пример 1.

В структуре рассматриваемой НСАУ задана её линейная часть (ЛЧ) оператором:

, где T₁=1,0c., T₂=0,5c., T₃=0,1c.