Современные проблемы автоматизации и управления
Лекции проф. для магистров
Лекция 9 (20. 11 2010), оригинал 19. 11. 2009г
Содержание предыдущей лекции. Оцениваются возможности и область применения, изложенного в предыдущей лекции, критерия абсолютной устойчивости нелинейных ДСАУ А. Гелига. Подробно изложен "модифицированный" круговой критерий абсолютной устойчивости нелинейных ДСАУ В. А. Якубовича (СП б). Модификация критерия состояла в получении условий его применения для оценки устойчивости систем с двухполярной широтро - импульсной модуляцией, которые успешно применяются в силовой электротехнике и электромеханике. Описаны основные варианты использования кругового критерия устойчивости для моделей нелинейных ДСАУ с двухполярными ШИП, которые интенсивно используют в этих устройствах, в качестве усилителей мощности.
Глава 5. Проблема устойчивости и колебательности моделей дискретных нелинейных систем автоматического управления.
5.1 Исходные положения
Содержание вопросов, которые мы будем изучать в этой главе, связано также с проблемой абсолютной устойчивости нелинейных ДСАУ. Но в этих системах и их моделях могут существовать как режимы асимптотической, так и колебательной устойчивости. Поэтому мы выдели новую главу.
При асимптотической устойчивости система в равновесии приходит в начало координат, где все ее производные движения и сами движения будут равны нулю. Но есть еще режим "орбитальной устойчивости", когда по окончанию переходного процесса система переходит в автоколебательное движение и величина на входе нелинейного элемента δ(t) принимает значение:
δ(t) = δ(t + T), где T = const.
Величина на входе нелинейности повторяется с периодом Т. Здесь могут возникать различные режимы с постоянным периодом Т, либо с постоянной частотой ω. Такие режимы называются колебательными.
В нашей научной школе мы достаточно много занимались изучением этой интересной научной проблемы. ( См., например, работы (49) и (50).)
5.2. Обобщенная структура системы и основы критерия.
В этой главе мы продолжим изучение критериев абсолютной устойчивости нелинейных ДСАУ с использованием модификации критерия В. М. Пòпова. В качестве первоисточника используем нижеуказанную работу А.Х.Гелига*) Обобщенная модель системы изображена на рис 1.9:
![]()
|
![]() y(t) g(t)
y(t) g(t)
|
f(σ) σ(t)
Рис. 1.9.Модель нелинейной ДСАУ
НЛЧ непрерывная линейная часть, F(σ)статическая нелинейность.
емые слушатели, различия нашего представления "инженеров - прикладников" о предмете аналитического исследования и "теоретиков математиков", на труды которых мы постоянно опираемся в своих работах. Я неоднократно напоминал, что мы пользуемся различной с ними символикой и терминологией. Но различия не только в этом, а в наших базовых образованьях и, возможно, в усвоенных (или сложившихся) способах мышления. В научных исследованиях (а диссертация магистра относится к такой категории работ) мы должны научиться не только "ссылаться", но и творчески использовать труды теоретиков. Наши знания математики и теории управления вполне достаточны для решения таких задач. Итак, приступаем к разбору работы А. Гелига (*). Этим же символом будем отмечать и номера формул из этой работы. Основная из них (1*) записана автором так:
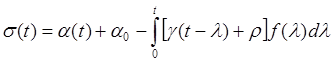 (1*)
(1*)
Здесь ![]() затухающая
и постоянная составляющие (по А. Гелигу) собственных колебаний
непрерывной линейной части системы,
затухающая
и постоянная составляющие (по А. Гелигу) собственных колебаний
непрерывной линейной части системы, ![]() затухающая и
постоянная составля
затухающая и
постоянная составля
________________________________________________________________________________
*) Гелиг А.Х. Метод усреднения в теории устойчивости нелинейных импульсных систем. Журнал АН СССР "Автоматика и телемеханика" №5, 1983 г.
ющие импульсной переходной
функции НЛЧ, ![]()
![]() сигналы
на входе и выходе нелинейности, названной автором - модулятором. Последнее
название удачно, поскольку здесь использована модель НДСАУ вида II (см. рис.5.
7 лекции 7) с нелинейным экстраполятором с широтно-импульсной или другими видами
нелинейной модуляции.
сигналы
на входе и выходе нелинейности, названной автором - модулятором. Последнее
название удачно, поскольку здесь использована модель НДСАУ вида II (см. рис.5.
7 лекции 7) с нелинейным экстраполятором с широтно-импульсной или другими видами
нелинейной модуляции.
Перепишем уравнение (1*) в знакомых нам символах и терминах (см. рис. 1. 9):
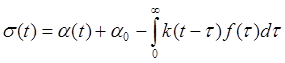 (1. 9).
(1. 9).
Здесь
![]() переменная и постоянная
составляющие собственных движений НЛЧ в ДСАУ.
переменная и постоянная
составляющие собственных движений НЛЧ в ДСАУ.
Теперь вспомним начальные лекции по линейной теории управления, - регулярные сигналы [f(τ)=δ(τ)] и реакция на них модели линейной системы
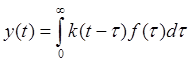 (2. 9)
(2. 9)![]()
Итак, в формуле (1. 9)имеем:![]() . Но что за остаток остался в этом
выражении α 0? В первоисточнике (*) указано, что
. Но что за остаток остался в этом
выражении α 0? В первоисточнике (*) указано, что ![]() для моделей НЛЧ с астатизмом.
Убедимся в этом
для моделей НЛЧ с астатизмом.
Убедимся в этом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.