Вычислительная среда Mathcad для решения системы уравнений

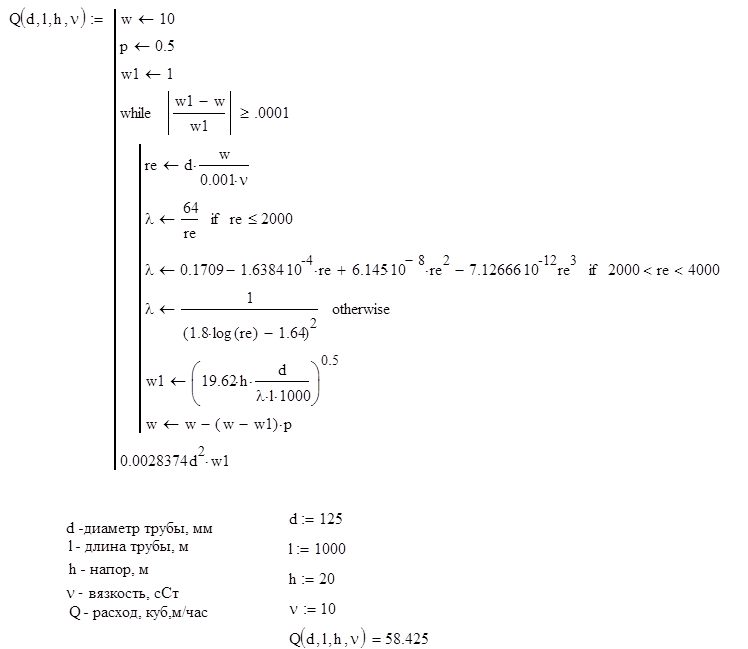
При аппроксимации функции несколькими зависимостями необходимо соблюсти точную стыковку участков не допуская разрывов.

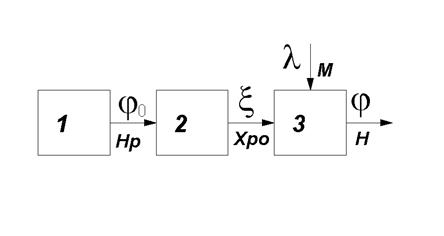
Задача 1 Построение расходных характеристик

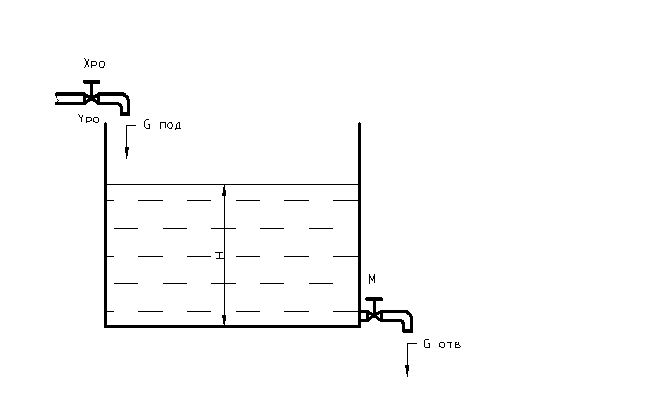
Имеется расходный бак, из которого расходуется то или иное количество жидкости, и в который по мере надобности такое же количество жидкости  добавляется.

Расход жидкости зависит от положения выходного крана М и уровня в баке Н.

При постоянной площади сечения трубопровода расход пропорционален скорости W.

Будем считать, что сопротивление на выходе сосредоточено в выходном кране М.

Тогда   

Подвод жидкости не зависит от уровня Н, а зависит только от входной координаты регулирующего органа Хро.

Известно, что:

-  при расчетном уровне Н=4 Gотв =2.

- в равновесном состоянии при максимальном открытии впускного и выпускного кранов уровень в баке Н = 4

Задание:

- определить,  какому принципу управления соответствует данная системы, считая выходной координатой уровень жидкости в баке

-построить расходные характеристики подвода и отвода жидкости для диапазона допустимых значений уровня жидкости Н от 3 до 5 и для трех разных положений кранов на входе и на выходе (коэффициенты сопротивления соотносятся как 1, 2, 3.

-предложить изменения в структурной схеме, улучшающие свойства системы регулирования.

Нахождение передаточного коэффициента по стороне отвода К1

Gотв=К1*М*,  где М - нагрузка, задаваемая положением регулирующего органа на отводе.

Полное открытие регулирующего органа соответствует относительному значению нагрузки M=1

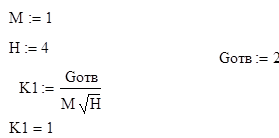
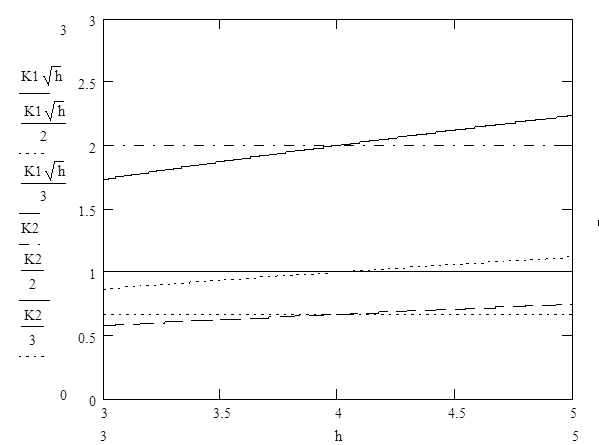
В системе реализуется принцип разомкнутого управления:

 

Методическое указание к составлению уравнения графика и построению графика переходного процесса для динамического звена первого порядка

Применение оператора дифференцирования к расчету переходной характеристики звена первого порядка

Для  решения дифференциального уравнения удобно ввести оператор дифференцирования D.

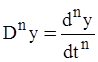
К оператору дифференцирования применимы обычные правила алгебры в случае операций с константами и операций возведения его самого в положительную степень. Запишем дифференциальное уравнение второго порядка в виде:

aD²y+bDy+cy=0

Чтобы данное уравнение превратилось в обычное квадратное уравнение необходимо, чтобы в производной повторялась сама функция y, и производные отличались только показателями степени константы перед повторяемой общей частью. Единственной функцией, отвечающей данным условиям, является функция y=Ae^mx. Тогда дифференциальное уравнение преобразуется к виду:

aAm²· e^mx + bAm· e^mx+ cA· e^mx =0

A· e^mx (am² + bm + c ) =0

Уравнение (am² + bm + c ) =0 называется характеристическим.

Корни характеристического уравнения вычисляются по формуле:

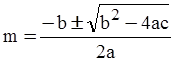
Если b² > 4ac, существует два действительных корня α  и β. Решение в общем виде можно записать так:

y=Ae^{α x}+ Be^{β x}

Если b² = 4ac, существует два равных корня α. Решение в общем виде можно записать так:

y = (A + B) e^{α x}

Если b² < 4ac, существует два комплексных  корня этого уравнения α  и β. Решение записывается в виде:

y = (Acos βx + Bsin βx) e^{α x}

Константы А и В определяются граничными условиями.

Рассмотрим систему первого порядка

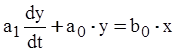
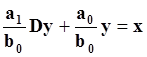
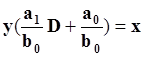
Характеристическое уравнение получается путем замены оператора дифференцирования на алгебраическую переменную m и приравнивания x к 0.

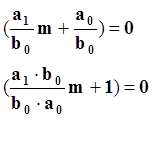
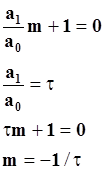
Тогда решение уравнения для переходного режима y=Ae^mt  примет вид: y=Ae^-t/τ .

Рассмотрим теперь скачек на входе в систему.

Для установившегося режима величина Dy равна 0, x = 1, y/x=b₀/a₀. Эти условия дают частное решение уравнения:

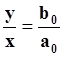
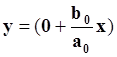
Следовательно, в общем виде решение уравнения будет представлять собой сумму:

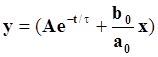
Найдем величину А, исходя из граничных условий: при t = 0 y = 0 x =1

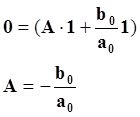
Отсюда  полное решение уравнения для переходного  и установившегося режима примет вид:

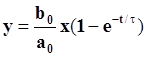
График переходной функция для звена первого порядка при b₀ = a₀ показан на рис.

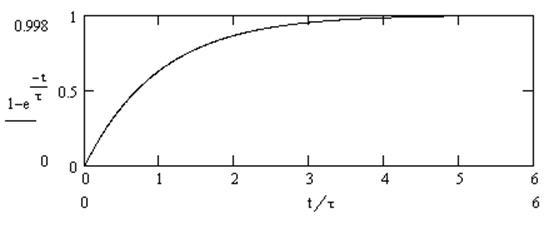
Через промежуток времени, равный 5 τ, соотношение между  выходным и входным сигналом установится постоянным и равным b₀/a₀.

В системах терморегулирования ДВС в качестве управляемой координаты используется температура среды. Ее замер осуществляется динамическим звеном первого уровня. Рассмотрим пример, когда датчик температуры, находящийся в потоке жидкости с температурой Т подвергается резкому изменению температуры жидкости до значения Т₁. Датчик температуры – термопара, помещенная в гильзу, заполненную маслом с массой m и теплоемкостью c. Будем считать, что теплопередача линейно зависит от разности температур.

Скорость передачи тепла к датчику:

dQ/dT =k(T₁-T)