Вычислительная среда Mathcad для решения системы уравнений, страница 2

Одновременно количество воспринятого датчиком тепла δQ, подведенного за время δt, приведет к изменению его температуры на величину δT в соответствии с выражением:

δQ = m·c· δT

Тогда

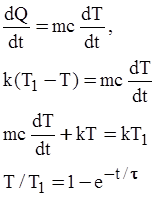
где τ =mc/k

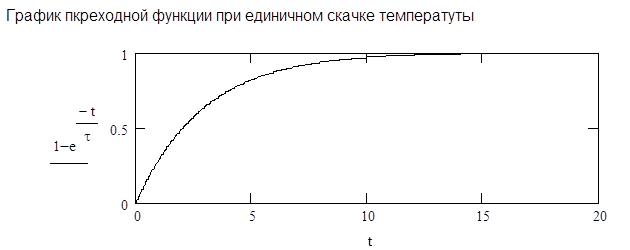
Так как в конце переходного периода  температуры потока и датчика выравниваются, т.е. Т / Т₁=1, график переходной функции не будет зависеть от температуры.

Задача 2 Составление уравнения и построение графика переходного процесса для динамического звена первого порядка

Имеется  чувствительный элемент датчика температуры, размещенный в трубопроводе. Датчик находится в защитной гильзе, заполненной маслом. Гильза имеет диаметр 5мм и длину 50 мм.

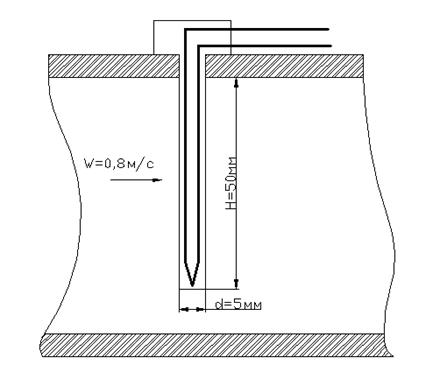
Считается, что температура масла соответствует температуре чувствительного элемента. Датчик помещен в поток воды со скоростью 0,8 м/с.

Коэффициент теплопередачи рассчитывается по формуле:

Уравнение теплопередачи в дифференциальной форме

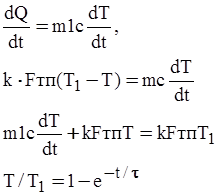
Постоянная времени τ, в секундах:

Методические указания по расчету характеристик динамического звена второго порядка

Применение преобразования Лапласа для расчета характеристик звена второго порядка

Колебательное звено относится к динамическим звеньям второго порядка и описывается дифференциальным уравнением:

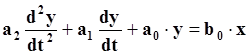
Как следует из правил преобразования по Лапласу, вторая производная функции y(t)  преобразуется в трехчлен:

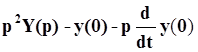, первая производная преобразуется в двучлен:

, где y(0) – значение функции при t = 0.

Вычитание двух функций а₀y – b₀x преобразуется в a₀Y(p)-b₀X(p).

Если  при t = 0 y(0) = 0 и 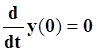, дифференциальное уравнение преобразуется в алгебраическое:

a₂p²Y(p)+ a₁pY(p)+a₀Y(p)=b₀X(p)

Передаточная функция:

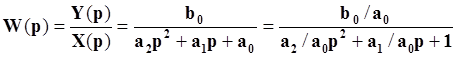
Учитывая, что b₀/a₀ – это передаточная функция в статическом режиме W,

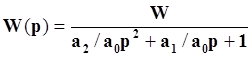
Дальнейшие преобразования сводятся к искусству разложения многочлена на множители. Принимая во внимание, что звено второго порядка может быть записано через величины собственной частоты колебания ω и коэффициент затухания σ,

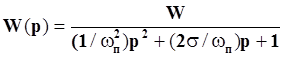
Рассмотрим выходной сигнал при скачкообразном сигнале на входе.

Так как X(p) = 1/p,

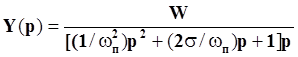
После преобразований выражение принимает следующий вид:

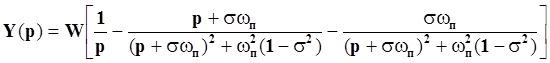
При критическом затухании, т.е. при σ = 1,

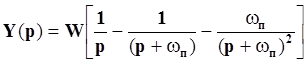
Используя таблицу преобразований Лапласа, конвертируем решение, полученное в Лапласовой форме, в функцию, зависящую от времени:

Примером системы второго порядка является пружинная система с демпфированием (рис.1).   

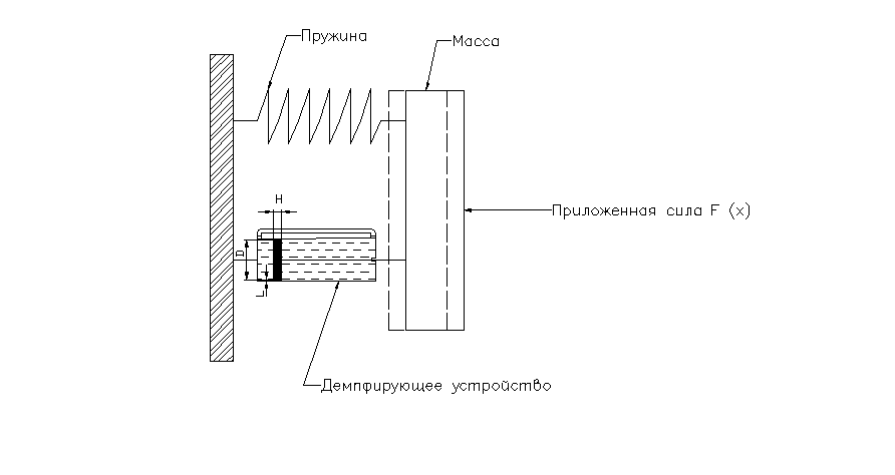
Рис.1

Система включает три основных элемента: массу, пружину и демпфирующее устройство – поршень, перемещающийся в цилиндре, заполненном маслом.  Входным сигналом является сила F, выходным – длина пружины y .Результирующая сила, действующая на массу m, равна разности приложенной силы F, силы упругости пружины (от растяжения или сжатия), и силы демпфирующего устройства.

Сила упругости пружины пропорциональна изменению ее длины y, т.е. ее можно представить в виде ky, где k – коэффициент жесткости пружины.

Сила демпфирующего устройства будет пропорциональна скорости перемещения поршня, т.е. ее можно представить в виде c(dy/dt), где с –константа.

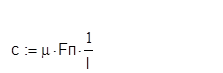
где μ – коэффициент динамической вязкости жидкости, l – зазор между трущимися поверхностями, F_п – поверхность трения.

Результирующая сила R, действующая на массу m, будет равна:

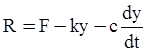
По второму закону Ньютона эта сила заставляет массу двигаться с ускорением. Т.к. ускорение – производная скорости, а скорость – производная перемещения (dy/dt)

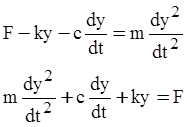
В случае отсутствия демпфирующего устройства масса, прикрепленная к концу пружины,, будет колебаться с собственной частотой

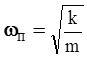
Колебательные системы характеризуются коэффициентом затухания σ, определяемым как:

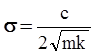
Тогда уравнение движения системы приобретает вид:

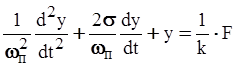
Задача 3  Расчет переходной функции звена второго порядка с помощью преобразования Лапласа

Пружинная система с демпфированием (рис. 1)состоит  из:

-пружины с коэффициентом жесткости k=1н/м;

- прикрепленной массы m=4кг;

- системы демпфирования с поршнем, двигающимся в цилиндре с маслом, имеющей следующие характеристики: коэффициент динамической вязкости касторового масла

m = 1,2 кг/сек м; диаметр поршня D = 5 см, высота поршня  H = 5см, зазор между поршнем и цилиндром l =1мм.

Требуется;

- найти частоту собственных колебаний пружины с массой m и коэффициент затухания колебаний

-  изменить размеры демпфирующей системы с целью получения коэффициента затухания колебаний равного 1.

Расчет системы демпфирования

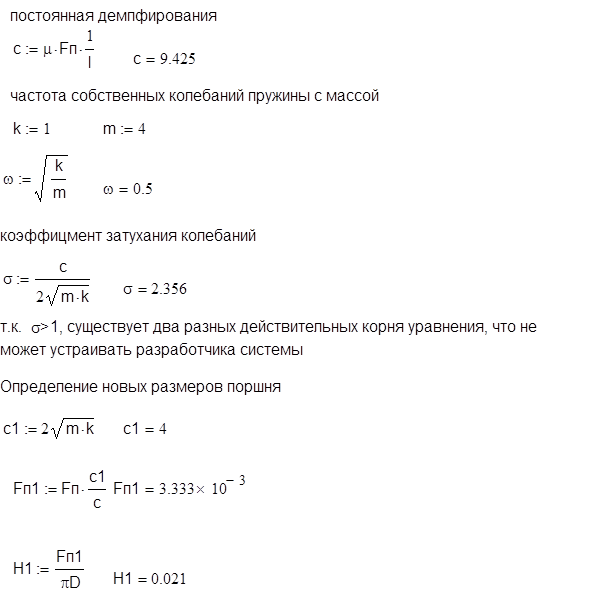
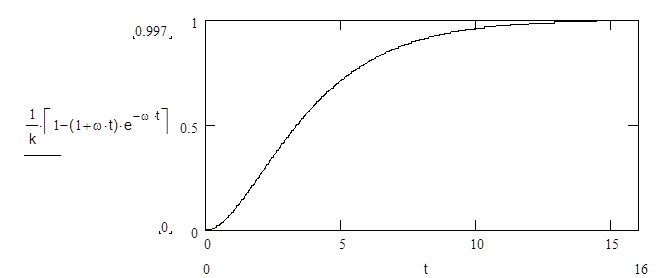
Переходная функция строится для единичного скачка входной координаты – приложенной к пружине силы F, следовательно  F = 1.

по преобразованию Лапласа

y/F=1/k[1-exp(-wt)(1+wt)]

График переходной функции