Проблема устойчивости и колебательности моделей дискретных нелинейных систем автоматического управления, страница 2

Пример. Пусть передаточная функция (ПФ) НЛЧ имеет такой вид:

 Методом "неопределенных коэффициентов" разобьем K(s) на слагаемые

K(s)= Из записи уравнений для числителя, найдем:

 . Следовательно, . Оба слагаемых в выражении K(s) безразмерны, что дает основание считать разложение выполненным правильно. Из ПФ в виде суммы найдем импульсные переходные характеристики k₁ (t) и k₂ (t).

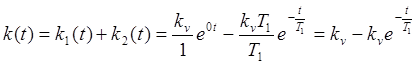.                                             (3. 9)

Таким образом, первое слагаемое в выражении (3. 9) и есть . Следовательно, ранее в пояснениях к формуле (2. 9) мы допустили неточность. Необходимо было записать:

                                                                               (4. 9)

Итак, я (С.К.) полагаю, что уравнение (4. 9) отражает свободное движение НЛЧ системы при воздействии на неё нелинейной части. Для астатических НЛЧ

Разрешим формулы (2*) и (3*) из работы (*), поменяв номера и символы:

,                                                                            (5. 9)

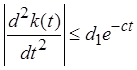.                                                                          (6. 9).

1)  Если найдем производную и возьмем t=0, то e⁰=1, тогда можем определить с₁.

2)  Тем же способом, найдя второю производную, вычисляем d₁.

3)  Задавая различные значения "с", получим нужную экспоненту. Например, если в формуле (5. 9) задать ct=5,5 то

Формулы (4*) оценивают пределы значений величины и её производной, а (5*) длительность сигналов выхода модулятора при различных формах и родах  нелинейной модуляции, т. е. характеризуют нелинейность F(σ).

5. 3  Критерий абсолютной устойчивости  дискретных систем с любыми видами нелинейной модуляции А. Гелига.

Будем исследовать абсолютную устойчивость статических и астатических моделей НДСАУ с  ШИМ 1-го рода. Тогда важны выражения (6*) - (8*). Они характеризуют сигнал f(t) на выходе усилителя мощности в модели реальной НДСАУ.

,           где  среднее значение кусочно - непрерывного сигнала на выходе усилителя мощности модулятора

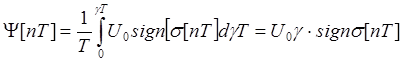 ,                                                  (7. 9)

где U₀γ – среднее значение импульса напряжения на выходе усилителя.

Не уверен, (С. К.), "хорошо ли это"? Но этим усреднением перешли от нелинейной ШИМ к линейной АИМ. Для этого в работе (*) существенных обоснований нет.

Основное предположение о законе модуляции заключается в следующем.

Для любого n, существует,, и справедливо неравенство:

                                                                (8. 9).

Основная формула, по которой ведется оценка абсолютной устойчивости НДСАУ – (9*). Она подобна критерию устойчивости В. М. Пóпова. Этот критерий устойчивости для непрерывных нелинейных систем записывают так:

.                                                                                   (9. 9).

В работе (*) для исследования моделей НДСАУ эта формула записана иначе и преобразована нами к следующему  виду:

,                                                        (10. 9)

где  для статических систем, но для астатических систем.

Неравенство (10, 9) названо А. Гелигом теоремой. При выполнении неравенства модель НДСАУ будет абсолютно устойчива, если соблюдены следующие условия и положения:

1. Для астатических систем ρ>0, а для статических ρ=0, кроме того, если размерность  то размерность .  псевдочастотная а. ф. х. преобразованной статической .НЛЧ (Она названа А. Гелигом "   некритической составляющей переходной функции НЛЧ") (См. пример 1).

2. Если , то существует функция , удовлетворяющая условию Липшица (11. 9) с постоянным коэффициентом "l"

                  ,                                                     (11. 9)

где

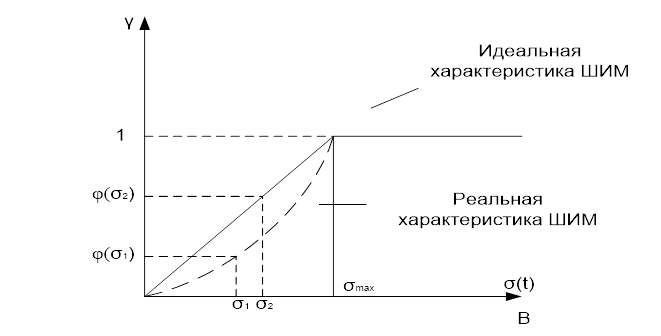
Условие (11. 9) поясняется рисунком 2. 9, где изображены графики идеального и реального широтно-импульсного модуляторов. Реальный модулятор работает с запаздыванием, что обусловлено необходимостью преобразования напряжения сигнала σ в ширину импульса γ и дальнейшее преобразование ширины импульса в напряжение выхода усилителя мощности .

Рис.2.9. Статические характеристики нелинейности, совместно с усилителем мощности.

3. Для определения числа δ необходимо вычислить неравенство:

,                                                                (12. 9)

где:

       

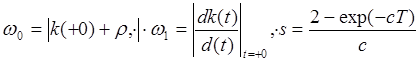
В пояснениях к неравенству (12. 9) обозначено:

причем в случае прямоугольных импульсов напряжения на входе НЛЧ можно, по мнению А. Гелига, положить:

                  (13. 9)

При выполнении условия абсолютной устойчивости (8. 9), каковы бы не были начальное значение убывающей функции α(t) и α₀,=0, входной сигнал , а при α₀,==const

______________________________________________________________________________________

*⁾Я (С.К.) с подозрением отношусь к этой формуле, думаю, что должно быть:.

Естественно, нелинейность должна принадлежать классу «0-К», что и подтверждают неравенство (8. 9) и рис. 3. 9

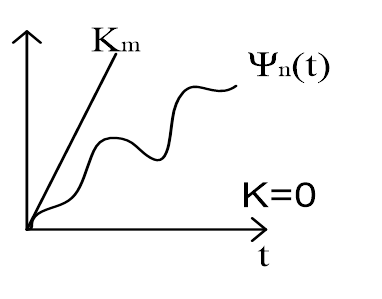
Рис. 3. 9. Нелинейная функция на выходе усилителя мощности в модели НДСАУ

Оформила:                   Беляева Н. И.   05.11.2009.

Скорректировано 05 - .12.01.2011.