Среднее время безотказной работы. Среднее время восстановления. Коэффициент готовности. Среднее время безотказной работы

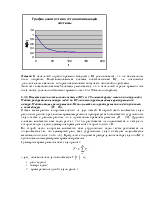
Раздел 5.3 ТФРВС

5.3.1. Имеется вычислительная система из 10 элементарных машин (ЭМ) (основная подсистема 9 ЭМ, одно восстанавливающее устройство). Одна ЭМ восстанавливается за 24 часа и безотказно работает в среднем 1000 часов. Вычислить математические ожидания времени безотказной работы θ и восстановления вычислительной системы T. Пояснить результат.

Средним временем безотказной работы вычислительной системы (средней наработкой до отказа) называется величина

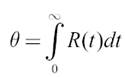
Где R(t) – функция надёжности – вероятность того, что производительность ВС, начавшей функционировать в состоянии i (n≤i≤N), равна на промежутке времени[0, t) производительности основной подсистемы.

θ  характеризует среднее время, которое ВС, начавшая функционировать в исправном состоянии, проработает без сбоя.

Средним временем восстановления вычислительной системы называется величина 

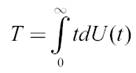
Где U(t) - функция восстановимости – вероятность того, что в ВС, имеющей начальное состояние i (0≤i<n), будет восстановлен на промежутке времени [0, t) уровень производительности основной подсистемы.

Т  характеризует среднее время, за которое ВС, начавшая функционировать в неисправном состоянии, восстановит работоспособность.

Для расчета θ и T используется “частотный” метод. Среднее время безотказной работы ВС равно

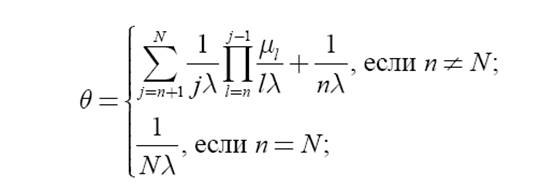
Среднее время восстановления ВС определяется выражением

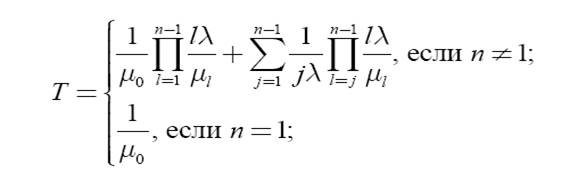
где величины m_l, l = 0,…, N – 1 , рассчитываются по формулам

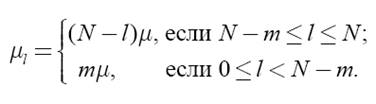
Дано:N=10 – общее число ЭМ вычислительной системы;

n=9 – число ЭМ основной подсистемы ВС, ;

m=1 – число восстанавливающих устройств, ;

m=1/24 – интенсивность восстановления ЭМ;

λ = 1/1000 – интенсивность потока отказов ЭМ.

Подставляем в формулу:

Т.к. l = n = 9 рассчитываем: 

θ =  574 часа

=

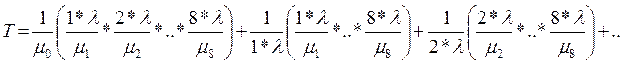
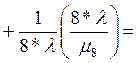
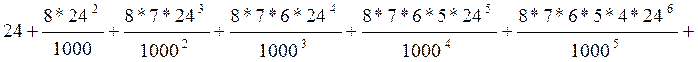
29,5 часов

Ответ:в среднем вычислительная система выйдет из строя через 574 часа, т.е в конкретный момент времени в отказавшем состоянии может находиться только одна машина. 29,5 часов – среднее время, через которое элементарных машин станет >= 9, при условии, что в начальный момент времени их было <9.

5.3.2. Имеется вычислительная система (ВС) из 10 элементарных машин (ЭМ) (основная подсистема 9 ВМ, одно восстанавливающее устройство). Одна ЭМ восстанавливается за 24 часа и безотказно работает в среднем 1000 часов. Рассчитать коэффициент готовности системы S. Пояснить результат.

S(t) – функция готовности – вероятность того, что в системе, начавшей функционировать в состоянии i(i =) в момент времени tпроизводительность будет равна производительности основной подсистемы.

Предел функции готовности  называется коэффициентом готовности:

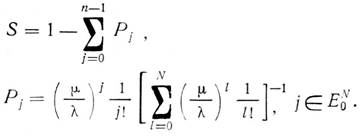
Коэффициент готовности самый распространённый показатель, характеризующий функционирование ВС в стационарном режиме. Он информирует о том, как быстро можно ожидать восстановление требуемой производительности, в случае если система достаточно долго эксплуатируется.

S =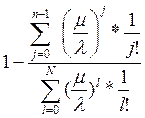

S= 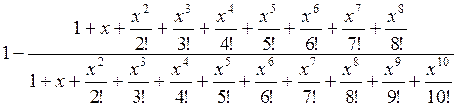, где x =  m /λ.

Дано:N=10 – общее число ЭМ вычислительной системы;

n=9 – число ЭМ основной подсистемы ВС, ;

m=1 – число восстанавливающих устройств, ;

m=1/24 – интенсивность восстановления ЭМ;

λ = 1/1000 – интенсивность потока отказов ЭМ.

Подставляем в формулу

S=1-  

=0,95

Ответ: Вероятность того, что система в стационарном режиме находится в работоспособном состоянии, т.е. будет работать не меньше 9 машин из 10, равна 0,95.

5.3.3. Имеется живучая вычислительная система из 5 элементарных машин (ЭМ) (основная подсистема 4 ЭМ, одно восстанавливающее устройство). Одна ЭМ восстанавливается за 24 часа и безотказно работает в среднем 1000 часов. Рассчитать вектора среднего времени безотказной работы { θ_k }и среднего времени восстановления   { T k } вычислительной системы, k =4,5 . Пояснить результат.

Вектором среднего времени безотказной работы(средней наработки до отказа) вычислительной системы называется вектор Θ = {θ_n, …, θ_N}, где

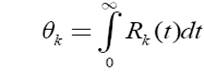
θ характеризует среднее время, которое ВС, начавшая функционировать в исправном состоянии, проработает без сбоя.

Вектором среднего времени восстановления вычислительной системы называется векторT = {T_n, …, T_N}, где

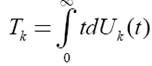
Т  характеризует среднее время, за которое ВС, начавшая функционировать в неисправном состоянии, восстановит работоспособность.

Для расчета этих показателей используются формулы (n заменяется на k):

Среднее время безотказной работы ВС равно

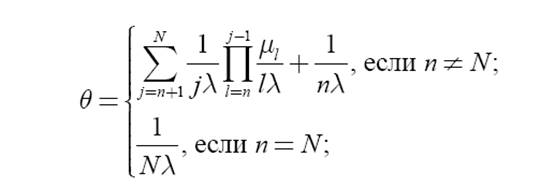
Среднее время восстановления ВС определяется выражением

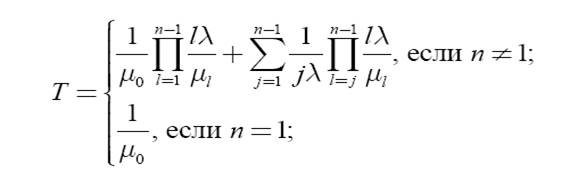
где величины m_l, l = 0,…, N – 1 , рассчитываются по формулам

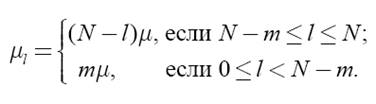
Дано:N=5 – общее число ЭМ вычислительной системы;

n=4 – число ЭМ основной подсистемы ВС, ;

m=1 – число восстанавливающих устройств, ;

m=1/24 – интенсивность восстановления ЭМ;

λ = 1/1000 – интенсивность потока отказов ЭМ.

Подставляем в формулу:

Т.к. l = n = 4, то

θ₄ =  (1 / (5* (1/ 1000 )))*( (1/24) / (4/1000) ) +1/(4/ 1000 ) = 2333 часа