Среднее время безотказной работы. Среднее время восстановления. Коэффициент готовности. Среднее время безотказной работы, страница 4

Распределение: {2,1,15,16}; {4,3,5,13,14}; {9,10,11,12,6,7,8,17,18}

5.3.6. Имеется вычислительная система (ВС) из 10 элементарных машин и набор одноранговых задач. Найти распределение набора задач по ВС, минимизирующее общий штраф за задержку решения задач набора. Найти общий штраф.

Теорема:

I =

Указанная последовательность I обеспечивает минимизацию функции штрафа тогда и только тогда, когда выполняется следующее условие , где i₁ – номер задачи, которая решится первой.

1          2         3         4        5        6        7         8        9         10       процессоры

F(I) = 3*7 + 4*3 + 5*1 + 3*2 + 5*2 = 21+12+5+6+10 = 54

5.3.7. Имеется вычислительная система из 10 элементарных машин (ЭМ) (основная подсистема 9 ЭМ, одно восстанавливающее устройство). Одна ЭМ восстанавливается за 24 часа и безотказно работает в среднем 700 часов. Вычислить математические ожидания времени безотказной работы θ и восстановления вычислительной системы T. Пояснить результат.

Средним временем безотказной работы вычислительной системы (средней наработкой до отказа) называется величина

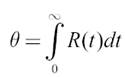
Где R(t) – функция надёжности – вероятность того, что производительность ВС, начавшей функционировать в состоянии i (n≤i≤N), равна на промежутке времени[0, t) производительности основной подсистемы.

θ  характеризует среднее время, которое ВС, начавшая функционировать в исправном состоянии, проработает без сбоя.

Средним временем восстановления вычислительной системы называется величина 

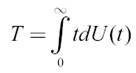
Где U(t) - функция восстановимости – вероятность того, что в ВС, имеющей начальное состояние i (0≤i<n), будет восстановлен на промежутке времени [0, t) уровень производительности основной подсистемы.