Среднее время безотказной работы. Среднее время восстановления. Коэффициент готовности. Среднее время безотказной работы, страница 6

При отсутствии избыточных машин (k=5) среднее время безотказной работы составляет 140 часов, что почти в 10 раз меньше, чем если есть резерв. Среднее время восстановления 27,6 часов - среднее время, через которое элементарных машин станет = 5, при условии, что в начальный момент времени их было <5.

5.3.10. Имеется живучая вычислительная система (ВС) из 10 элементарных машин (ЭМ) (основная подсистема 9 ЭМ, одно восстанавливающее устройство). Одна ЭМ восстанавливается за 24 часа и безотказно работает в среднем 700 часов. В начальный момент времени исправно 9 ЭМ. Рассчитать функции потенциальной живучести N(i,t) и занятости восстанавливающей системы ВС M(i,t). Построить их графики. Вычислить коэффициенты потенциальной живучести N и занятости восстанавливающей системы ВС M. Пояснить результат.

Функцией потенциальной живучести ВС называется величина

, где  - математическое ожидание производительности ВС в момент t при условии, что в момент начала функционирования в системе было i работоспособных ЭМ, ; - показатель производительности одной ЭМ.

Функция потенциальной живучести – средняя производительность ВС.

Функцией занятости восстанавливающей системы называется величина

, где  - математическое ожидание числа занятых восстанавливающих устройств в момент t при условии, что ВС начала функционировать в состоянии i, .

Функция занятости восстанавливающей системы – средняя загруженность ВС.

Коэффициентом потенциальной живучести вычислительной системы и коэффициентом занятости восстанавливающей системы называются величины соответственно

  = ,

 =

Расчёт функции потенциальной живучести и функции восстанавливающей в случае, когда восстанавливающая система имеет высокую производительность, выполняют по формулам:

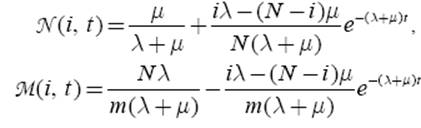
Условие высокой производительности системы:

Дано:N=10 – общее число ЭМ вычислительной системы;

n=9 – число ЭМ основной подсистемы ВС, ;

m=1 – число восстанавливающих устройств, ;

m=1/24 – интенсивность восстановления ЭМ;

λ = 1/700 – интенсивность потока отказов ЭМ.

Условие высокой производительности выполняется: 0,010,04.

t	N	M
0	0,900	1,000
20	0,939	0,614
40	0,955	0,451
60	0,962	0,382
80	0,965	0,353
100	0,966	0,340
120	0,966	0,335
140	0,967	0,333
160	0,967	0,332
180	0,967	0,332
200	0,967	0,332

N =0.967; M = 0,332.

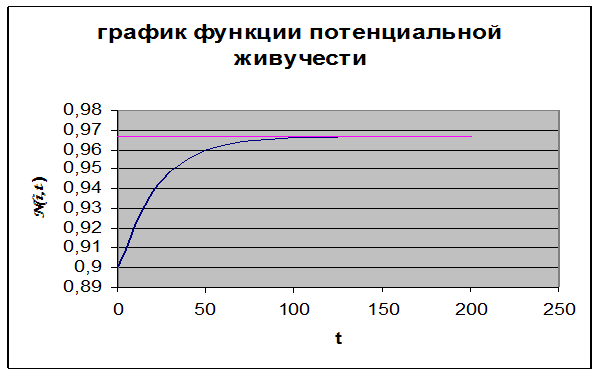
Ответ: В начальный отрезок времени живучесть ВС увеличивается, т.к. не все машины были исправны. Восстанавливающая система восстанавливает ВС, т.е. появляются дополнительные машины, которые обеспечивают живучесть основной подсистемы.

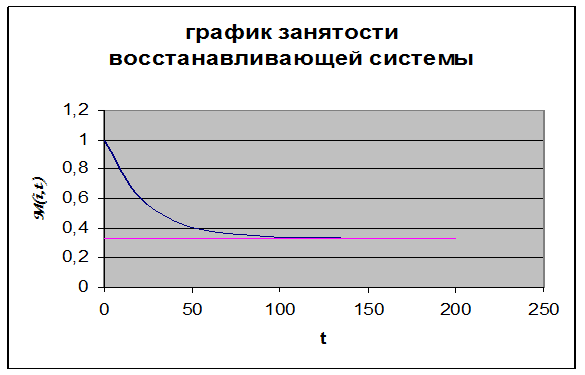
Занятость восстанавливающей системы уменьшается, т.к. в начальный отрезок времени она была занята (в начальный момент времени лишь 9 из 10 машин исправны).

5.3.11. Имеется вычислительная система (ВС) из 10 элементарных машин и набор задач. Найти распределение набора задач по ВС, минимизирующее общее время решения набора. Найти общее время решения. Использовать алгоритм решения задачи упаковки в контейнеры (Θ = 100).

Общая схема работы алгоритма состоит из двух частей. В первой части множество задач различных рангов с различным временем решения преобразуется во множество укрупнённых задач также с разным рангом, но с одинаковым временем решения (Θ = 50). Другими словами, множество всех задач ранга r, 1rn, разбивается на подмножества, в каждое из которых входят задачи, суммарное время решения которых близко к Θ.

Во второй части алгоритма множество всех укрупнённых задач также разбивается на подмножества так, что суммарный ранг всех укрупнённых задач в каждом подмножестве максимально близок к n (n = 8). В результате получается распределение набора задач по ВС с субоптимальным суммарным временем решения.

Суммарное время решения всех задач ранга r: