Агротехнические показатели трактора. Продольная устойчивость трактора. Статическая устойчивость от опрокидывания, страница 7

Схождение колес. Наклон колеса к поверхности качения вызывает боковой увод его в сторону наклона, т. е. колеса стремятся разойтись: левое — налево, правое — направо. Поверхность качения колеса формирует поверхность конуса, а не цилиндра, что вызывает проскальзывание и интенсивное изнашивание шин. Для устранения этого явления вводят схождение колес (рис. 8.10, б). Расстояние А между колесами впереди делают меньше (на 1-4 мм в автомобилях и на 2-8 мм в тракторах), чем расстояние В сзади. Касательные и боковые реакции дороги, а также удары, действующие на колеса, стремятся вызвать их отрицательное схождение. В связи с наличием зазоров в рулевой трапеции и других соединениях управляемым колесам придается несколько большее схождение, чем необходимо из условий компенсации только развала колес.

Нарушение регулировок устройств стабилизации управляемых колес в эксплуатации сказывается на износе шин.

8.4. Поворот гусеничного трактора

8.4.1. Кинематика поворота трактора с одинарным

 потоком мощности в трансмиссии

Поворот гусеничного трактора осуществляется за счет рассогласования скоростей гусениц, одной из которых (забегающей) придают более высокую скорость по сравнению с другой (отстающей). Движение трактора на повороте можно рассматривать как вращательное в плоскости опорной поверхности вокруг мгновенного центра О (рис. 8.12). При этом каждая из гусениц по мере перемещения по дуге окружности радиусом R₁или R₂поворачивается на некоторый угол вокруг своего центра поворота — соответственно О₁ и О₂. Центр поворота трактора и мгновенные центры поворота каждой из гусениц расположены на одной линии O—O₁—O₂, которая в общем случае соединяет центры давления гусениц и не совпадает с поперечной осью а—а, проходящей через середины опорной поверхности гусениц.

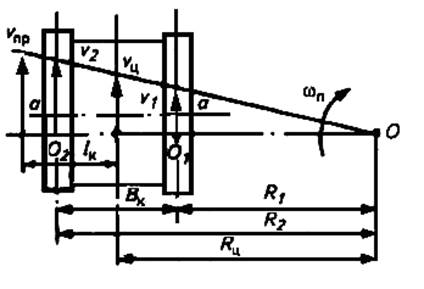
Рисунок 8.12 - План скоростей при движении гусеничного трактора на повороте

План скоростей движения и геометрического центра трактора представлен на рисунке 8.12. В зависимости от скоростей движения забегающей и отстающей гусениц радиусы поворота можно выразить, пользуясь правилом подобия треугольников, следующими зависимостями:

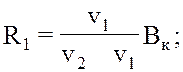
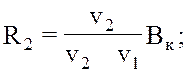
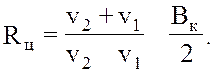                   (8.3)

Радиус поворота часто представляют в виде относительной величины, за единицу длины которой принята половина ширины колеи тракторов:

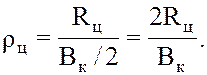
Тогда

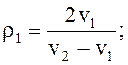
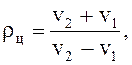
а угловая скорость поворота трактора

В зависимости от типа механизма поворота возможны три варианта движения трактора на повороте в сравнении с режимом прямолинейного движения: скорость точки геометрического центра трактора снижается (V_ц<V_пр); скорость на повороте равна скорости прямолинейного движения (V_д=V_пр); скорость на повороте  уменьшается до нуля (V_ц=0), трактор поворачивается на месте при одинаковой скорости гусениц, вращающихся в противоположные стороны.

Механизм поворота с дифференциалом. Простой дифференциал, используемый в качестве механизма поворота, при подтормаживании одной из полуосей (рис. 8.13) уменьшает скорость v₁ гусеницы с приводом от этой полуоси, увеличивая в соответствующей пропорции скорость v₂ и сохраняя скорость v_ц на повороте равной скорости прямолинейного движения трактора. Это следует из второго свойства дифференциала.

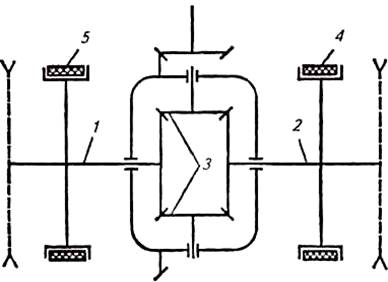
Рисунок 8.13 - Схема механизма поворота с простым дифференциалом: 1,2 — полуоси; 3 — дифференциал; 4,5— тормоза

Кинематику поворота рассмотрим в предположении, что при переходе от прямолинейного движения к повороту частота вращения вала двигателя и буксование гусениц не изменяются.

Минимальный радиус поворота центра машины можно определить, пользуясь выражением (8.3). При полном торможении одной из полуосей (ω₁=0) другая будет вращаться с удвоенной угловой скоростью: ω₂ = 2ω_о. Тогда

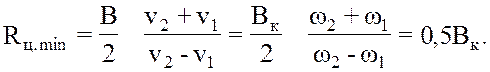
Таким образом, простой дифференциальный механизм, используемый в качестве механизма поворота, кинематически обеспечивает поворот гусеничного трактора с минимальным радиусом, равным половине ширины колеи, т. е. вокруг центра отстающей гусеницы.