Тягово-скоростные свойства и топливная экономичность автомобиля с гидромеханической трансмиссией. Особенности гидродинамических передач, страница 8

Суммарный инерционный момент двигателя и насосного колеса

                         (6.24)

где J_д.н - суммарный момент инерции двигателя и насосного колеса ГП;  - векторы угловых скоростей соответственно насосного и турбинного колес.

Если насосное колесо соединено с коленчатым валом двигателя непосредственно, то их угловые скорости одинаковы, т.е. . В этом случае

,                                       (6.25)

где J_д - момент инерции двигателя, определяемый так же, как и при механической трансмиссии; J_н - момент инерции насосного колеса с учетом моментов инерции всех деталей, кинематически связанных с ним, включая массу жидкости в полости насосного колеса.

При установке согласующей передачи между двигателем и гидротрансформатором момент инерции J_д.н вычисляется по формуле

(6.26)

где i_с.п - передаточное число согласующей передачи: i_с.п=ω_д/ω_н; J_с.пi - момент инерции i-й вращающейся массы согласующей передачи; i_i - передаточное число от i-й массы до насосного колеса.

Инерционный момент турбинного колеса

                                      (6.27)

где J_т - момент инерции турбины с учетом массы жидкости в ее полости.

Выразим угловую скорость ω_т через скорость автомобиля v:

                                        (6.28)

где i_тр – передаточное число механической части трансмиссии между ГП и ведущими колесами автомобиля.

Подставим значение ω_т в выражения (6.24) и (6.28):

                                 (6.29)

                                    (6.30)

Тогда выражение (6.23) примет вид:

         (6.31)

При использовании аналитических методов оценки тягово-скоростных свойств автомобиля производная dn_н/dn_твычисляется с помощью метода численного дифференцирования.

При установившемся движении автомобиля

                                  (6.32)

Сравнивая выражение (6.31) с аналогичным выражением (2.29) для автомобиля с механической трансмиссией и учитывая выражение (2.38) получаем формулу для определения коэффициента приведённой массы автомобиля с гидромеханической трансмиссией:

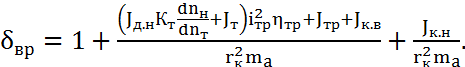           (6.33)

Для непрозрачного ГT dn_н/dn_т=0, поэтом δ_вр значительно меньше, чем у автомобиля с механической трансмиссией.

6.7. Динамическая характеристика автомобиля с гидромеханической трансмиссией

При построении динамической характеристики автомобиля с гидромеханической трансмиссией значения динамического фактора D и скорости v автомобиля вычисляются по формулам:

                       (6.34)

                                  (6.35)

Для вычисления D и v используется выходная характеристика М_т=f(n_т) системы ДВС-ГТ (или системы ДВС-ГМ).

Динамическая характеристика автомобиля с гидротрансформатором (рис. 6.11) существенно отличается от динамической характеристики автомобиля с механической трансмиссией (рис. 4.2). В связи с этим определение отдельных показателей тягово-скоростных свойств автомобилей с гидромеханической и механической трансмиссиями производится по-разному.

У автомобиля с ГМП значения динамического фактора на передачах достигают максимумов при нулевой скорости. Поэтому для автомобиля с гидротрансформатором вместо D_н.max и D_в.max определяют условные максимальные динамические факторы соответственно на низшей D_н.ymax и на высшей D_в.ymax передачах. Значения этих показателей вычисляют при М_т=М_т.э и n_т=n_т.э. Преодолеваемые автомобилем уклоны определяют с учетом значений D_н.уmax и D_в.уmax. При оценке максимального уклона i_max выбирают меньшее из значений, вычисляемых на основе выражений:

                              (6.36)

                                     (6.37)

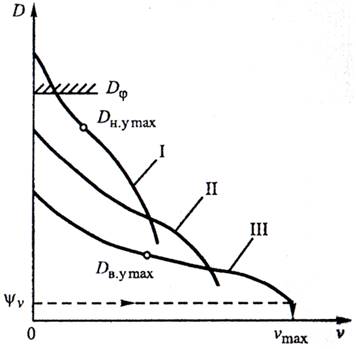
Рисунок 6.11 – Динамическая характеристика автомобиля с гидротрансформатором

Значение D_в.ymax характеризует величину уклона, при котором автомобиль может осуществлять движение на высшей передаче неограниченное время, поскольку КПД гидротрансформатора при этом не ниже η_гт=0,8.