Значения i и Kт соответствуют принятым табличным значениям λн, использованным при решении уравнения (6.16). По результатам вычислений осуществляется построение искомых выходных характеристик Мт=f(nт) и Nт=f(nт), а также характеристики ηгт=f(nт) и графика кинематической характеристики гидродинамической передачи nн=f(nт).
На рисунке 6.8 показаны выходные характеристики системы двигатель-гидротрансформатор.
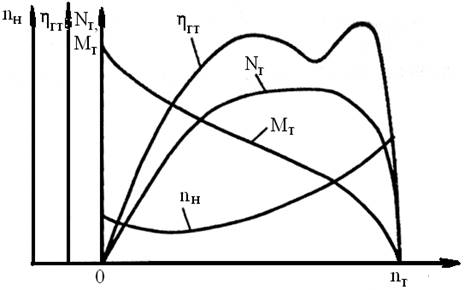
Рисунок 6.8 – Выходная характеристика системы двигатель-гидротрансформатор
Сравним выходную характеристику ДВС-ГТ с внешней скоростной характеристикой двигателя (рис. 6.9). Двигатель может устойчиво работать при изменении частоты вращения в интервале nм≤nд≤nххmax. Частота вращения вала турбины может изменяться в пределах 0≤nт≤nтmax. При этом обеспечивается устойчивая работа двигателя во всем диапазоне изменения частоты вращения его вала от nххmin до nххmax. Форма характеристики Мт=f(nт) приближается к идеальной, показанной штриховой линией.
В эксплуатационном диапазоне использования характеристики гидротрансформатора (при ηгт≥0,8) момент на валу турбины изменяется в пределах Мт.э≥Мт≥Мт.м, где Мт.э – момент, соответствующий ηгт.э; Мт.м - момент соответствующий переходу на режим гидромуфты. Частота вращения турбины при этом изменяется в интервале nт.э≤nт≤nт.м.
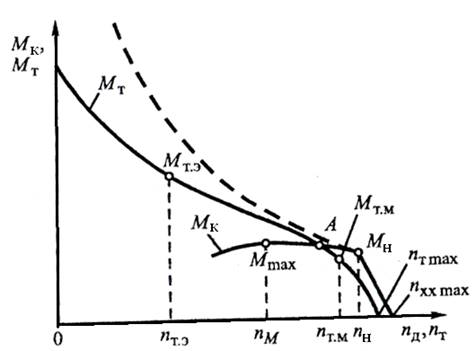
Рисунок 6.9 - Сравнение характеристик Мт=f(nт) и Мк=f(nд):
- - - - идеальная характеристика
Коэффициент приспособляемости системы ДВС-ГТ по моменту определяется по формуле
(6.21)
а коэффициент приспособляемости по угловой скорости (частоте вращения вала турбины)
(6.22)
Значения 
находятся в пределах 1,6-2,5, а значения 
- в пределах 2,0-2,6. Поскольку 
существенно больше значений 
двигателя, это позволяет уменьшить количество
ступеней в механической коробке передач и упростить ее конструкцию.
Выходные характеристики системы ДВС-ГМ получают таким же образом, как и для системы ДВС-ГТ. Рассмотрим некоторые особенности выходной характеристики Мт=f(nт) этой системы. Так как у ГМ Кт=1 на всех режимах, то Мт=Мн=Мд. Поэтому характеристики Мт=f(nт) строят на одном и том же графике, что и характеристики совместной работы ДВС и ГМ Мн=f(nн) и Мд=f(nд).
Характеристика Мт=f(nт) существенно отличается от характеристики двигателя Мд=f(nд) (рис. 6.10), поскольку существует при любых значениях nт, в том числе и при nт=0. Следовательно, ГМ не позволяет двигателю остановиться при любой нагрузке. Она предотвращает возникновение больших динамических нагрузок и предохраняет двигатель и трансмиссию от перегрузок.
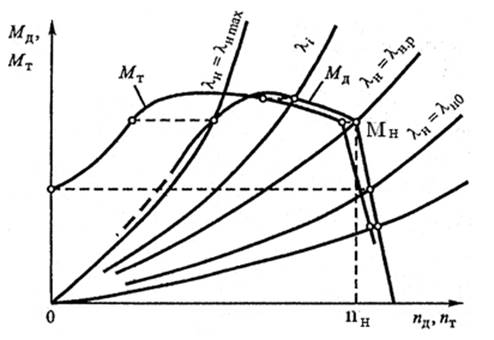
Рисунок 6.10 – Характеристика системы двигатель-гидромуфта
Активный диаметр ГМ выбирают из условия, чтобы при Nеmax скольжение ГМ не превышало 3 %, т.е. i≥0,97.
Желательно, чтобы безразмерная характеристика ГM λн=f(i) имела участок обратной прозрачности, а λн0 было значительно меньше λнmax. В этом случае при отпущенной педали акселератора момент на турбине будет сравнительно небольшой, что позволит останавливать автомобиль у светофора без выключения передачи в коробке передач. Это обеспечивает быстрое и в то же время плавное, без рывков и больших динамических нагрузок, трогание автомобиля с места и его разгон, а также упрощение управления автомобилем.
6.6. Дифференциальное уравнение движения автомобиля с гидромеханической трансмиссией
Дифференциальное уравнение прямолинейного движения автомобиля с гидромеханической трансмиссией аналогично уравнению для автомобиля с механической трансмиссией, только вместо характеристики двигателя Мк=f(nд) в нем используется выходная характеристика Мт=f(nт) системы ДВС-ГТ. С учетом этого дифференциальное уравнение имеет вид
(6.23)
При определении коэффициента приведенной массы δвр автомобиля с гидродинамической передачей необходимо дополнительно учесть влияние, моментов инерции насосного и турбинного колес на изменение кинетической, энергии системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.