Исследование переходных процессов в линейных цепях. Моделирование переходных процессов на ПК. Обработка графиков, страница 9

С

Кл

R

Кл

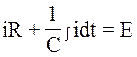
                                                                    .                                      (7.6)

Е

Е

                                             Это линейное дифференциальное уравнение. Для решения  

i (t)

                                              используем, рассмотренный выше, классический метод.

                            1-ый пункт: Нахождение корней характеристического

Рис.7.16. Цепь R-С.

                           уравнения.

Составляем схему для нахождения корней. По конфигурации это после-         коммутационная схема, в которой все источники э.д.с. “закорачивают”, источники тока разрывают, резисторы оставляют без изменения, а емкости заменяют сопротивлением 1/pС . Полученная схема показана на рис.7.17. По методу контурных токов составляем  уравнение:      

R

                                                        I₁₁(R+1/рС)=0.

I11

1/рС

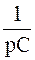
                                   Характеристическое уравнение     R+ =0               (7.7)

Рис.7.17 Схема к п.1     Находим корень 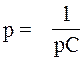 ,    размерность корня

2-ой пункт: Расчет принужденного режима (t→ ∞)

Составляем расчетную схему в принужденном режиме. Так как действует источник постоянной э.д.с., то в принужденном режиме это будет цепь постоянного тока, а по-этому i_Cпр=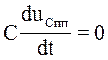 и емкость следует в данном случае “разорвать”. Расчетная схема показана на рис.7.18.                             I_ПР=0.

Записывая уравнение по 2-ому закону Кирхгофа,

R

                                                                    I_ПРR+U_CПР=Е ,

UCпр

E

Iпр

                                                         получим     U_CПР=Е.

Рис.7.17 Схема к п.1  

3-ий пункт: Записываем решения для искомых токов и напряжении.

Так как корень один, то решения  следует искать в виде:

i(t)= I_пр +A₁e^pt,       u_L(t)= 0+ A₂e^pt                                       (7.8)

A₁, A₂- постоянные интегрирования, подлежащие определению. Для этого, прежде всего запишем (7.8) в момент коммутации, т.е при t=0. Получим:

i(0)= I_пр +A₁,       u_С(0)= 0+ A₂, где                                            (7.9)

i(0), u_С(0)- начальные значения (условия) тока в цепи и напряжения на емкости в момент коммутации. Найдя i(0), u_С(0), определим A₁, A₂

4-ый пункт: Рассчитываем независимые начальные условия.

Необходимо определить напряжение на емкости- u_С(0). Согласно 2-му закону коммутации  u_C(-0)=u_C(0)  (напряжение на емкости непрерывно).

На практике это  означает, что для определения u_С(0)надо рассчитать докоммутацион-   ную схему,  найти напряжения на емкостях в момент коммутации u_C(-0). В рассматриваемом случае схема была отключена от источника, а следовательно напряжение на емкости было равно нулю. В результате u_C(-0)=u_C(0)=0.

Знание u_C(0), позволяет определить постоянную А₂ (см.7.9). Чтобы определить А₁, надо рассчитать i (0), а это зависимое начальное условие

5-ый пункт: Рассчитываем зависимые начальные условия.