Исследование переходных процессов в линейных цепях. Моделирование переходных процессов на ПК. Обработка графиков, страница 15

A.Теоретические сведения.

Исходная схема имеет вид (рис.7.26). Обсудим расчет этой схемы. В рассматри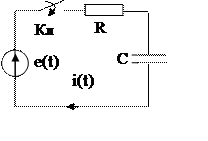                                              аемой (послекоммутационной) схеме, одна ветвь, один                                             контур. Следовательно, можно составить одно уравнение по 2-ому закону Кирхгофа для мгновенных значении:

                                                         (7.18)

Если сравнить уравнение (7.6) и (7.18),  то они отличаютРис.7.26. Цепь R-С.      ся только правой частью. Напомним, что от вида правой части зависит только одна (из двух) составляющая решения линейного дифференциа-льного уравнения- принужденная часть решения. Если для решения уравнения (7.18) использовать классический метод, то очевидно, весь порядок остается без изменения.

Необходимо лишь заново рассчитать принужденный режим. Поэтому, пропуская 1-ый пункт (Нахождение корней характеристического уравнения), приступим сразу ко 2-ому пункту: Расчет принужденного режима (t→ ∞).

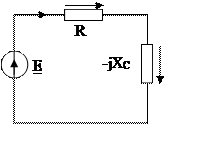
Характер принужденного режима определяется в линейной цепи видом э.д.с. В рассматриваемом случае e(t)=E_msin(ωt+γ), т.е. это синусоидальная функция. Но, если э.д.с. меняется по синусоидальному закону, то расчет принужденного режима следует выполнить символическим методом (см.лаб.раб. №2). Расчетная схема принужденно- го режима показана на  рис.7.27. По закону Ома в символической фор ме  получим:

IПР

URПР

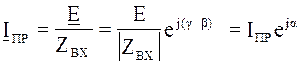                                                ,                           (7.19)

UСПР

                                                                                 

где:Z_ВХ=R-jX_C= ,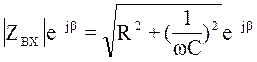

Рис.7.27 Схема к п.2

                                                          ,

U_CПР =I_ПР (-jX_C)=I_ПР (-j=I_ПР()e^j(α-90) .     (7.20)

Комплексу тока (7.19) соответствует функция времени  i_ПР(t)=I_ПРsin(ωt+α)  (7.21)

Комплексу напряжения (7.20)  u_CПР(t)= I_ПР()sin(ωt+α-90^○)  (7.22)

3-ий пункт: Записываем решения для искомых токов и напряжении.

Выполнение данного пункта не имеет принципиальных отличий, с аналогичным пунктом для схемы R-L. Проделайте его самостоятельно.

4-ый пункт: Рассчитываем независимые начальные условия

Так как схема была отключена  то имеют место нулевые независимые  нача- льные условия: U_C(-0)=U_C(0)=0.

5-ый пункт: Рассчитываем зависимые начальные условия.

Расчет зависимых начальных условии можно провести двумя способами: а) Составить систему уравнений по законам Кирхгофа для мгновенных значении в послекоммутационной схеме и рассчитать ее при t=0 (в момент коммутации). В рассматриваемом случае, уравнение составлено (7.18). Записываем его при t=0

  Так как  u_C(0)=0, то i(0)R =E_msinγ     i(0)= 

б) второй способ состоит в расчете схемы в момент времени t=0.

Расчетная схема показана на рис.7.28.а. Так как Е_С=U_C(0)=0 схему можно пре- 

R

R

                                                                                  образовать к виду ( рис.7.28б).   

ЕС

e(0)

e(0)

                                                                                   По закону Ома получаем:  

i(0)

i(0)

                                                                                                                                                                          а                                           б