Проектирование новой железнодорожной линии с пересечением постоянного водотока мостовым переходом, страница 3

pЭ, %	= 2		= 4
	KР	Qt	KP	Qt
0,1	2,34	5119	2,76	6038
0,3	2,15	4704	2,41	5273
0,5	2,05	4485	2,28	4988
1	1,92	4201	2,06	4507
3	1,71	3741	1,76	3851
5	1,60	3500	1,62	3544
10	1,44	3150	1,43	3129
20	1,26	2757	1,24	2713
30	1,14	2494	1,11	2428
40	1,05	2297	1,02	2232
50	0,96	2100	0,94	2057
60	0,88	1925	0,87	1903
70	0,80	1750	0,80	1750
80	0,72	1575	0,73	1597
90	0,61	1335	0,65	1422
95	0,53	1160	0,58	1269
97	0,48	1050	0,55	1203
99	0,40	875	0,49	1072

       Далее не специальную клетчатку вероятности наносят точки с координатами (р, Q_T) и получают теоретические кривые распределения Q_T = f(p).

       На эту же клетчатку вероятностей наносят эмпирические точки с координатами (р_э, Q_T). Для дальнейшего рассмотрения принимается та из двух теоретических кривых распределения вероятностей, которая имеет наименьшее отклонение от эмпирических точек (наилучшим образом с ними согласуется).

       В рассматриваемом примере это теоретическая кривая распределения вероятностей для соотношения 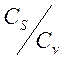= 4

      Пользуясь теоретической кривой распределения вероятностей, можно определить максимальные годовые расходы на водотоке Q любой вероятности превышения, а по графику Q=f(H) определить соответствующий данному расходу уровень УВВ.

       Так как в рассматриваемом примере мостовой переход проектируется для железной дороги общего пользования 2 категории, то расчетный определяется с вероятностью превышения 1%, а наибольший – с вероятностью превышения 0,33%.

       Как видно из графика клетчатки вероятности, расход с вероятностью превышения 1% - Q_1% составляет 4507 м³/с, а с вероятностью 0,33% Q_0,33% - 5273 м³/с.

       По величине расходов и графику зависимостей расходов от отметки горизонтов воды определены соответствующие им уровни высокой воды (УВВ), а по этим уровням с помощью остальных графиков зависимостей – необходимые расчетные данные, приведенные в таблице №6.

Значения	Вероятность 1%				Вероятность 0,33%
	Весь поток	Главное русло	Правая пойма	Левая пойма	Весь поток	Главное русло	Правая пойма	Левая пойма
УВВ	расчетный (РУВВ) = 408,9				наибольший (НУВВ) = 409,2
Расход Q, М3 /с	4507	4232	65	210	5273	4810	150	303
Средняя скорость v, м/с		3,92	0,65	0,95		4,15	0,80	1,08
Площадь ω, м	1400	1070	100	220	1605	1155	170	280
Контроль		3,96	0,65	0,95		4,16	0,88	1,08
Ширина участка морфоствора b, м	669,0	314,0	149,5	205,5	684,0	314,0	152,5	217,5

      Таким образом, отверстие мотового перехода рассчитывается на безопасный пропуск расчетного расхода Q_1% = 4507 м³/с при РУВВ_1% = 408,9 м, а высота пойменных насыпей и струенаправляющих дамб определяют с учетом подьема воды до отметки НУВВ_0,33% =409,2 м (Q_0,33% - 5273 м³/с).

5.  Установление пределов варьирования отверстием моста на основе общего размыва подмостового русла

       Отверстием моста в свету L называется расстояние между передними гранями устоев (или между откосами конусов при обсыпных устоях), определяемое на отметке РУВВ, за вычетом суммарной величины ширины промежуточных опор.

       Сужение водного потока в месте расположения мостового перехода при паводке приводит к увеличению скорости течения воды под мостом. В свою очередь увеличение скорости потока приводит к размыву русла в подмостовом сечении, величина которого характеризуется коэффициентом размыва Р:

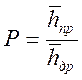
где средняя глубина потока под мостом после размыва, м;

       средняя глубина потока под мостом до размыва, м.

       Средняя глубина потока под мостом после размыва определяется по эмпирической формуле

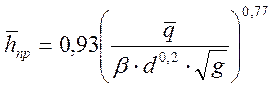
где - средний удельный расход воды под мостом;

        d – средний диаметр частиц несвязанного грунта;

        b - параметр, зависящий от вероятности превышения расхода, принимается по таблице №7 

              ниже;

         g – ускорение свободного падения g = 9,81м/с².

Вероятность превышения расхода, %	2	1	0,33
Параметр b	0,97	1,0	1,07

          Средний расход воды под мостом определяется по формуле:

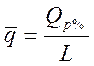
где Q_p% - расчетный расход заданной вероятности превышения;

       L – отверстие моста,м.

       Средняя глубина потока под мостом до размыва по формуле

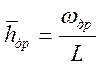
где площадь живого сечения, м², под мостом до размыва при РУВВ_р% в пределах

                 рассматриваемого отверстия моста.

       Таким образом, задаваясь различными значениями величины отверстием моста L и размещая его в пределах живого сечения реки с учетом положения русла, геологии и других условий, определяется площадь живого сечения под мостом до и после размыва и значение коэффициента размыва Р.