Проектирование новой железнодорожной линии с пересечением постоянного водотока мостовым переходом, страница 2

       Под заданной вероятностью превышения или, как принято говорить, обеспеченностью, подразумевается та вероятность превышения, при которой должны быть найдены расчетный и максимальный расходы. Заданные вероятности – величины нормируемые, степень допускаемого риска при их назначении устанавливается с учетом многих факторов: гидрологических, гидравлических, экономических, связанных со стоимостью восстановлением сооружений, а также с учетом оценки потерь при остановки транспортного конвейера в случае отказа (перебоя в движении), сроков службы сооружения, условий их эксплуатации и д.р.

       Требуемые значения вероятностей превышения устанавливаются нормами проектирования сооружения и приведены в таблице №3 ниже:

Категория дороги	Вероятность превышения расходов и соответствующих им уровней воды на пике паводка
	расчетного	наибольшего
3 и выше	1:100(1%)	1:300(0,33%)
4	1:50(2%)	1:100(1%)
4 – подъездные пути к предприятиям не допускающим перерыва в движении поездов по условиям технологического производства	1:100(1%)	1:100(1%)

       Размер отверстия водопропускного сооружения определяется по расчетным расходам, а проверка сохранности его, а также расчет отметки бровки пойменных насыпей и незатопляемых регуляционных сооружений осуществляется по наибольшим расходам.

       Определение расходов и соответствующих им уровней воды заданной вероятности превышения производится по кривой распределения вероятностей, для построения которой нужен статический ряд многолетних наблюдений за расходами. В курсовом проекте таким статическим рядом являются расходы, соответствующие уровням воды, наблюдаемым на водотоке в месте мостового перехода за 15 лет.

       Отметки уровней воды за 15 лет наблюдения в месте мостового перехода уже известны. Расходы, соответствующие уровням УВВ (см. таблицу №2), определяются по графику зависимостей Q = f(H) (см. график зав. расходов от отметки воды). Расходы ранжируются в убывающем порядке – т.е. в таблице №4 отметки воды (графа 3) и соответствующие им расходы (графа 4) заносятся в убывающем порядке, а в графе 2 данной таблицы указывается порядковый номер года наблюдения за данным уровнем воды.

       В графу 5 таблицы №4 заносят значение эмпирической вероятности превышения для каждого члена ряда, определенное по формуле

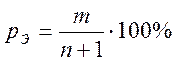
где m – порядковый номер члена ряда, расположенной по убывающей (графа 1)

       n – число наблюдений (в нашем случае n =15).

№ пп	Порядковый номер года наблюдения за УВВ	Отметки УВВ	Расход Q, м3/с	Эмпирическая вероятность pЭ, %	Модульный коэффициент Кi	(Ki - 1)2
1	2	3	4	5	6	7
1	8	408,72	3972	5,88	1,82	0,67
2	4	408,4	3250	11,76	1,49	0,24
3	7	408,25	2967	17,65	1,36	0,13
4	6	408,05	2567	23,53	1,17	0,03
5	15	408,02	2533	29,41	1,16	0,02
6	5	407,75	2200	35,29	1,01	0,00
7	16	407,75	2200	41,18	1,01	0,00
8	9	407,72	2167	47,06	0,99	0,00
9	14	407,65	1950	52,94	0,89	0,01
10	13	407,60	1933	58,82	0,88	0,01
11	1	407,55	1800	64,71	0,82	0,03
12	10	407,49	1700	70,59	0,78	0,05
13	2	407,45	1600	76,47	0,73	0,07
14	11	407,40	1500	82,35	0,69	0,10
15	3	407,25	1333	88,24	0,61	0,15
16	12	407,25	1333	94,12	0,61	0,15
Итого			35005			1,67

       Первый параметр случайной величины - среднеарифметическое значение расхода воды – определяется по формуле

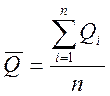
где ∑Q_i – сумма годовых максимальных расходов за все годы наблюдений.

       В рассматриваемом примере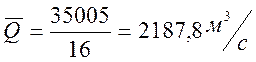

       В методике по определению гидрологических характеристик для удобства расчетов используется безразмерная величина – отношение наблюдаемого годового максимального расхода к среднеарифметическому – так называемый модульный коэффициент К_i:

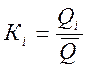
       Данный модульный коэффициент записывается в графу 6 таблицы №4.

       Вторым параметром случайной величины Q является коэффициент вариации (коэффициент рассеивания), характеризующий среднеквадратическое отклонение членов ряда, определяемый по формуле

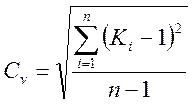
      В нашем варианте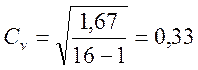

       Так как число наблюдений, задаваемое в курсовом проекте, мало, то третий параметр – коэффициент ассиметрии С_s, характеризующий среднекубическое отклонение, отпределяется косвенным путем из соотношения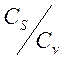

Задаваясь соотношениями величин 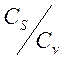(у нас 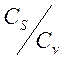=2 и 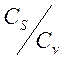=4), по таблицам приложений находят ординаты теоретических кривых распределения вероятностей К_Р и вычисляют теоретические расходы Q_T по формуле

       Результаты приведены в таблице №5.