причем ![]() . Равенство (39) можно
рассматривать как соотношение в кольце
. Равенство (39) можно
рассматривать как соотношение в кольце ![]() :
:
![]() (40)
(40)
Умножим
теперь первое уравнение системы (38) на ![]() и вычтем из него второе
уравнение, умноженное на
и вычтем из него второе
уравнение, умноженное на ![]() .
Мы получим уравнение
.
Мы получим уравнение
![]() ,
(41)
,
(41)
являющееся следствием системы (38).
При
условии, что значение неизвестного y не
обращается в нуль многочлен ![]() , исходная система уравнений
(38) эквивалентна системе, которая получается из нее заменой первого уравнения
уравнением (41). Однако среди решений системы (38) могут быть и такие, которые
обращают в нуль многочлен
, исходная система уравнений
(38) эквивалентна системе, которая получается из нее заменой первого уравнения
уравнением (41). Однако среди решений системы (38) могут быть и такие, которые
обращают в нуль многочлен ![]() . Эти решения совпадают с
решениями системы, которая получается из системы (38) добавлением уравнения
. Эти решения совпадают с
решениями системы, которая получается из системы (38) добавлением уравнения ![]() и заменой второго уравнения
уравнением
и заменой второго уравнения
уравнением ![]() , где
, где ![]() .
.
Таким
образом, множество решений системы (38) есть объединение множеств решений двух
систем уравнений: 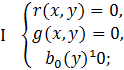
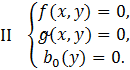 (Первая из этих систем наряду
с уравнениями содержит неравенство
(Первая из этих систем наряду
с уравнениями содержит неравенство ![]() ). Каждая из систем I и II
проще исходной системы уравнений в том смысле, что сумма степеней всех ее
уравнений по x меньше, чем у системы (38).
). Каждая из систем I и II
проще исходной системы уравнений в том смысле, что сумма степеней всех ее
уравнений по x меньше, чем у системы (38).
Применяя описанную выше процедуру к первым двум уравнениям каждой из систем I и II, а затем к уравнениям каждой из вновь получившихся систем и т.д. до тех пор, пока это возможно, мы, в конце концов, придем к ряду систем уравнений и неравенств, в каждой из которых лишь одно уравнение содержит неизвестное x. Каждая из получившихся систем уравнений и неравенств имеет вид
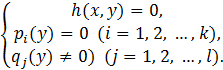 (42)
(42)
Для
решения системы (42) нужно, очевидно, найти общие корни многочленов ![]() , выбрать из них те, которые не
являются корнями ни одного из многочленов
, выбрать из них те, которые не
являются корнями ни одного из многочленов ![]() , а затем каждый из оставшихся
корней подставить в первое уравнение и решить полученное уравнение относительно
x.
, а затем каждый из оставшихся
корней подставить в первое уравнение и решить полученное уравнение относительно
x.
Таким образом, решение каждой из получившихся систем вида (42) сводится к последовательному решению алгебраических уравнений с одним неизвестным. Множество решений исходной системы (38) есть объединение множеств решений всех этих систем.
Пример 23. Решим систему уравнений:
![]()
Представим левые части уравнений как многочлены от x:
![]()
Разделим второе уравнение на
первое. Здесь ![]() ,
, ![]() ,
, ![]() . Для осуществления такого
деления необходимо домножить G(x)
на
. Для осуществления такого
деления необходимо домножить G(x)
на ![]() . Заметим, что
. Заметим, что ![]() . В противном случае из первого
уравнения получается противоречивое тождество
. В противном случае из первого
уравнения получается противоречивое тождество ![]() . Поэтому система уравнений
. Поэтому система уравнений ![]() равносильна исходной. При
делении
равносильна исходной. При
делении ![]() на F(x)
получается остаток
на F(x)
получается остаток ![]() . Исходная система эквивалентна
системе
. Исходная система эквивалентна
системе ![]() или (с учетом неравенства
или (с учетом неравенства ![]() )
) ![]() . Отсюда
. Отсюда ![]() ,
, ![]() ,
, ![]() . Тогда из первого уравнения
получаем
. Тогда из первого уравнения
получаем ![]() ,
, ![]() ,
, ![]() .
.
Если
воспользоваться теоремой 27, то система (38) будет иметь решение только в
случае, если многочлены F(x)
и G(x)
не взаимно просты и, значит, их результант ![]() равен нулю. Но результант
равен нулю. Но результант ![]() - это многочлен от одной
переменной y. Поэтому систему (38) можно
еще решить и так. Сначала найти все корни уравнения
- это многочлен от одной
переменной y. Поэтому систему (38) можно
еще решить и так. Сначала найти все корни уравнения ![]() от одной переменной y.
Подставить их в одно из уравнений системы (38). Получится уравнение от одной
переменной x. Решить его. Такой метод
называется методом исключения неизвестного при помощи результанта.
от одной переменной y.
Подставить их в одно из уравнений системы (38). Получится уравнение от одной
переменной x. Решить его. Такой метод
называется методом исключения неизвестного при помощи результанта.
Пример
24. Решим
систему уравнений из примера 23 методом исключения неизвестного при помощи
результанта. Составим результант ![]() и приравняем его к нулю:
и приравняем его к нулю: 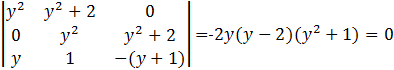 . Как мы видели ранее,
. Как мы видели ранее, ![]() - посторонний корень. Остальные
три - это
- посторонний корень. Остальные
три - это ![]() ,
, ![]() ,
, ![]() . Тогда из первого уравнения
получаем
. Тогда из первого уравнения
получаем ![]() ,
, ![]() ,
, ![]() .
.
Упражнение
20. Решить
систему уравнений: 1) ![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() ;
9)
;
9)![]() ;
10)
;
10)![]() .
.
Упражнение
1. Ответ: а) ![]() ,
,
![]() ; б)
; б) ![]() ,
,
![]() ; в)
; в) ![]() ,
,
![]() ; г)
; г) ![]() ,
,
![]() ; д)
; д)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.