взаимно просты, то существуют такие многочлены u и v, что
![]() ,
, ![]() ,
, ![]() .
(25)
.
(25)
Обратно, если
существуют многочлены u
и v, удовлетворяющие
условиям (25), то многочлен ![]() ,
являющийся общим кратным многочленов f
и g, имеет степень,
меньшую, чем степень произведения fg.
Степень наименьшего общего кратного в этом случае тем более меньше степени fg, и, значит, многочлены f и g не являются взаимно простыми.
,
являющийся общим кратным многочленов f
и g, имеет степень,
меньшую, чем степень произведения fg.
Степень наименьшего общего кратного в этом случае тем более меньше степени fg, и, значит, многочлены f и g не являются взаимно простыми.
Итак, вопрос о
взаимной простоте многочленов f
и g сводится к вопросу
о существовании многочленов u
и v, удовлетворяющих
условиям (25). Выясним, когда такие многочлены существуют. Запишем их в общем
виде: ![]() ,
, ![]() . Предположим для определенности, что
. Предположим для определенности, что
![]() . Каждое из произведений fu, gv представляет собой многочлен степени не
выше
. Каждое из произведений fu, gv представляет собой многочлен степени не
выше ![]() . Коэффициенты многочлена fu, записанные в столбец, имеют
вид
. Коэффициенты многочлена fu, записанные в столбец, имеют
вид
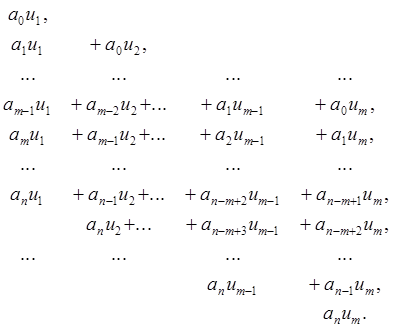
Коэффициенты многочлена gv имеют вид
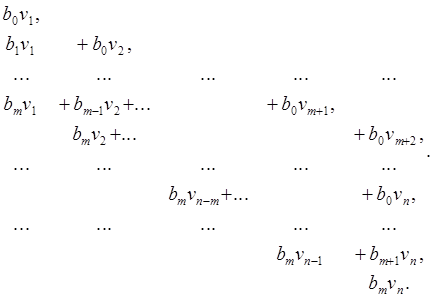
Приравнивая
коэффициенты многочленов fu
и gv при одинаковых
степенях x, получаем
систему однородных линейных уравнений относительно неизвестных ![]() . Число уравнений этой системы равно
. Число уравнений этой системы равно ![]() , т.е. числу неизвестных. Если
перенести все члены с
, т.е. числу неизвестных. Если
перенести все члены с ![]() в
левую часть, то получится следующая матрица коэффициентов при неизвестных:
в
левую часть, то получится следующая матрица коэффициентов при неизвестных:
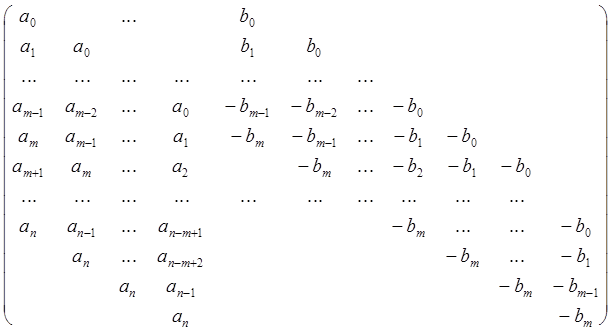
Рассматриваемая система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель этой матрицы равен нулю. При его вычислении можно для удобства умножить на -1 последние n столбцов и транспонировать матрицу. Полученный определитель
 (26)
(26)
называется результантом многочленов f и g.
Итак, доказана следующая теорема.
Теорема 27.
Многочлены ![]() не
являются взаимно простыми тогда и только тогда, когда их результант
не
являются взаимно простыми тогда и только тогда, когда их результант ![]() , определяемый формулой (26), равен
нулю.
, определяемый формулой (26), равен
нулю.
Замечание.
Если не предполагать, что коэффициенты a0, b0
отличны от нуля, то обращение в нуль определителя (26) остается необходимым
условием того, чтобы многочлены f
и g не были взаимно
просты. В самом деле, если f
и g не взаимно просты,
то существуют такие ненулевые многочлены u и v,
что ![]() ,
, ![]() ,
, ![]() . Поскольку мы не предполагаем, что
. Поскольку мы не предполагаем, что ![]() и
и ![]() , нельзя утверждать, что
, нельзя утверждать, что ![]() и
и ![]() , но, во всяком случае,
, но, во всяком случае, ![]() ,
, ![]() . Поэтому многочлены u и v тем более удовлетворяют условиям (25), а
из существования таких многочленов так же, как и выше, следует, что
определитель (26) равен нулю.
. Поэтому многочлены u и v тем более удовлетворяют условиям (25), а
из существования таких многочленов так же, как и выше, следует, что
определитель (26) равен нулю.
Пример 17.
Вычислим результант многочленов ![]() ,
,
![]() (с действительными
коэффициентами) и выясним, являются ли они взаимно простыми.
(с действительными
коэффициентами) и выясним, являются ли они взаимно простыми.
Искомый результант имеет вид
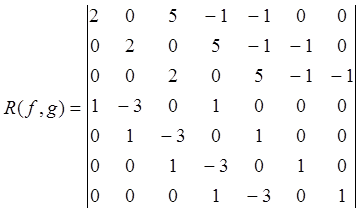
Вычисляя этот определитель, находим, что ![]() ; следовательно, многочлены f и g взаимно просты.
; следовательно, многочлены f и g взаимно просты.
Упражнение 14. При каком
значении ![]() многочлены имеют общий корень:
многочлены имеют общий корень:
1. ![]() и
и ![]() .
.
2. ![]() и
и ![]() .
.
3. ![]() и
и ![]() .
.
4. ![]() и
и ![]() .
.
5. ![]() и
и ![]() .
.
6. ![]() и
и ![]() .
.
7. ![]() и
и ![]() .
.
8. ![]() и
и ![]() .
.
9. ![]() и
и ![]() .
.
10. ![]() и
и
![]() .
.
11. ![]() и
и
![]() .
.
12. ![]() и
и
![]() .
.
13. ![]() и
и
![]() .
.
14. ![]() и
и
![]() .
.
В курсе математического анализа доказывается, что производная многочлена есть снова многочлен, причем если
![]() (27)
(27)
то
![]() .
(28)
.
(28)
В применении к
многочленам с коэффициентами из произвольного поля P определение производной, даваемое в
математическом анализе, теряет смысл, так как оно опирается на понятие предела.
Остается другой, формальный путь: принять формулу (28) за определение
производной. Коэффициент ![]() при
при
![]() в этой формуле следует
понимать как
в этой формуле следует
понимать как ![]() . Если
характеристика[1]
поля P равна нулю, то
. Если
характеристика[1]
поля P равна нулю, то ![]() для любого
для любого ![]() и, значит,
и, значит, ![]() при
при ![]() . В этом случае производная
многочлена степени
. В этом случае производная
многочлена степени ![]() является
многочленом степени
является
многочленом степени ![]() .
Напротив, если характеристика поля P
положительна, степень многочлена при дифференцировании может уменьшиться больше
чем на единицу. Может даже случиться, что производная многочлена положительной
степени будет нулевым многочленом. Например, пусть
.
Напротив, если характеристика поля P
положительна, степень многочлена при дифференцировании может уменьшиться больше
чем на единицу. Может даже случиться, что производная многочлена положительной
степени будет нулевым многочленом. Например, пусть ![]() . Тогда
. Тогда ![]() .
.
Докажем некоторые свойства дифференцирования многочленов с коэффициентами из кольца K.
Свойство 1.
Множитель ![]() можно вынести
за знак дифференциала.
можно вынести
за знак дифференциала.
[1]
Если все целые кратные единицы поля P являются
различными элементами поля P, т.е. ![]() при
при ![]() ,
то говорят, что поле P имеет характеристику нуль:
таковы, например, все числовые поля. Если же существуют такие целые числа k и l, что
,
то говорят, что поле P имеет характеристику нуль:
таковы, например, все числовые поля. Если же существуют такие целые числа k и l, что ![]() ,
но в P имеет место равенство
,
но в P имеет место равенство ![]() ,
то
,
то ![]() , т.е. в P
существует такое положительное кратное единицы, которое оказывается равным
нулю. В этом случае P называется полем конечной
характеристики, а именно
, т.е. в P
существует такое положительное кратное единицы, которое оказывается равным
нулю. В этом случае P называется полем конечной
характеристики, а именно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.