![]() , т.к.
, т.к. ![]() для воздуха.
для воздуха.
После введения диэлектрика разность потенциалов между обкладками найдем как:
![]() . (*)
. (*)
На
границе раздела воздуха и диэлектрика свободных зарядов нет, и в данном случае
вектор D
перпендикулярен границе раздела, поэтому вследствие граничных условий (![]() ): D2 = D1.
): D2 = D1.
Перепишем это через напряженности E1 и E2 с учетом диэлектрической проницаемости сред:
![]() .
.
Учитывая это, перепишем соотношение (*):
![]()
Значит,
![]()
Теперь
найдем ![]()
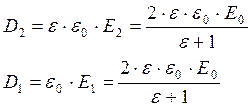
Найти энергию взаимодействия заряженного отрезка длиной l = 1.7 см и точечного заряда q = 3 мкКл, расположенного на продолжении этого отрезка на расстоянии а = 1 см от ближайшего конца. Линейная плотность заряда на отрезке t = 1 мКл/м.
Решение
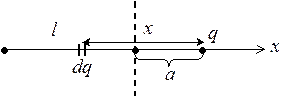 Энергию взаимодействия данной системы
проще всего посчитать как энергию заряда q, помещенного в определенную точку поля, создаваемого
заряженным отрезком:
Энергию взаимодействия данной системы
проще всего посчитать как энергию заряда q, помещенного в определенную точку поля, создаваемого
заряженным отрезком: ![]() .
.
Потенциал поля, создаваемого элементарными зарядами dq, выделенными на отрезке, найдется как сумма:
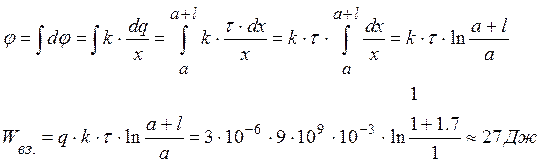
Металлический шар радиуса R несет заряд q. Шар окружен слоем диэлектрика толщиной d. Определить энергию электрического поля в слое диэлектрика и собственную энергию проводника.
Решение
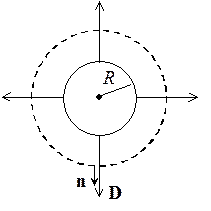 Найдем поле, создаваемое заряженным
шаром. Воспользуемся теоремой Гаусса для вектора D:
Найдем поле, создаваемое заряженным
шаром. Воспользуемся теоремой Гаусса для вектора D: ![]()
Из очевидной симметрии задачи в качестве замкнутой поверхности выберем сферу радиуса r, концентрическую с данным шаром.
![]()
Таким
образом, 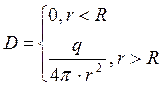
Учитывая связь между векторами D иE, получим:
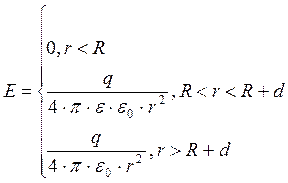
Тогда энергию поля, заключенного в слое диэлектрика, найдем по формуле:
![]() .
.
В
качестве элементарного объема dV
следует выбрать узкий сферический слой радиуса r и толщины dr,
где объемная плотность энергии почти не меняется: ![]() .
.
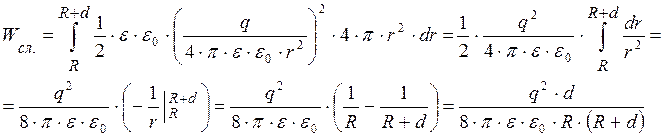
Собственную энергию проводника можно вычислить как энергию создаваемого им электрического поля, учитывая вычисленные значения напряженности в различных областях пространства:
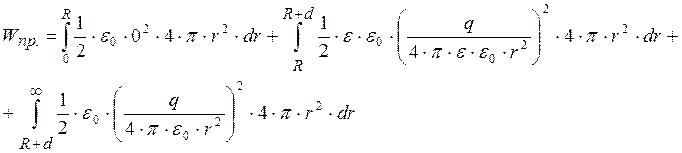
Второй интеграл был только что посчитан.
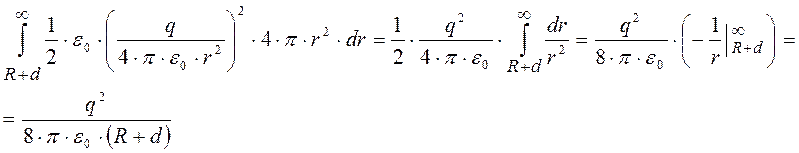
![]() .
.
Сфера радиуса R1 заряжена равномерно с зарядом q. Найти работу, совершенную электрическими силами, при увеличении радиуса сферы до R2.
Решение
 Работа электрических сил равна убыли
электрической энергии системы:
Работа электрических сил равна убыли
электрической энергии системы: ![]() .
.
Поле
сферы внутри нее равно 0, а снаружи совпадает с полем точечного заряда, которым
заряжена сфера, расположенным в центре этой сферы: ![]() .
.
Поэтому поле в области пространства, где r > R2, одинаково до увеличения радиуса сферы и после него. Поэтому и энергия в этой области пространства не изменяется. Изменение энергии происходит в области, где R1 < r < R2, т.к. после увеличения радиуса сферы до R2 напряженность поля, а вместе с ней и энергия поля, здесь становятся равными нулю. Поэтому:
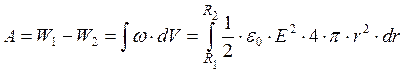 , где в
качестве элементарного объема выбран узкий сферический слой
, где в
качестве элементарного объема выбран узкий сферический слой ![]() из соображений
симметрии задачи.
из соображений
симметрии задачи.
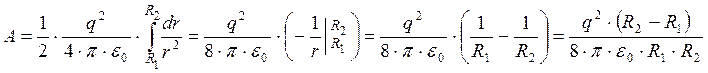
Внутри плоского конденсатора находится параллельная пластинка, толщина которой составляет h части зазора между обкладками. Емкость конденсатора в отсутствии пластинки С. Конденсатор с пластиной зарядили до напряжения U, затем отключили от источника и после этого медленно извлекли пластинку из зазора. Найти работу, затраченную на извлечение пластинки, если диэлектрическая постоянная ее материала e.
Решение
Работа по извлечению пластинки производилась против сил поля, поэтому:
![]()
W1 – энергия конденсатора с пластинкой,
W2 – энергия конденсатора без пластинки.
Емкость
воздушного плоского конденсатора ![]() .
.
Емкость конденсатора с диэлектрической пластинкой найдем как общую емкость двух последовательно соединенных конденсаторов:
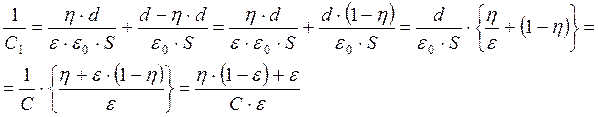
![]()
При отключении конденсатора от источника его заряд измениться не может:
![]()
Энергию конденсатора с диэлектрической пластинкой найдем по формуле:
![]()
Энергию конденсатора без диэлектрической пластинки найдем по формуле:
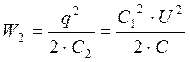
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.