Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле, страница 3

и его емкость: .

Если заряд (или систему зарядов) поместить у безграничной проводящей незаряженной плоскости, то между ними возникнет взаимодействие вследствие появления на этой плоскости индуцированных зарядов.

Поле в полупространстве, где расположен заряд, можно найти как сумму полей исходного заряда и «заряда-изображения» в данной плоскости. «Заряд-изображение» ищется из условия, что потенциал результирующего поля на проводящей поверхности должен обратиться в 0.

Емкостью системы проводников называется

, если проводники имеют заряды q разного знака.

Емкость плоского конденсатора: , где S – площадь его пластин, d – расстояние между ними.

При последовательном соединении конденсаторов емкость системы определяется:

При параллельном:

Примеры решения задач

Задача №1

Находящаяся в вакууме круглая очень тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью s. Найти потенциал и напряженность электрического поля на оси пластинки как функцию расстояния х от ее центра.

Решение

Потенциал в точке А, расположенной на оси на расстоянии х от центра пластинки будем искать как 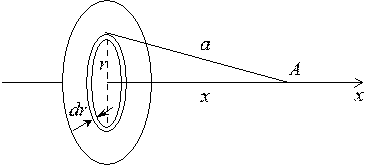потенциал системы зарядов .

Разобьем пластинку на тонкие кольца радиуса r и толщины dr. На этом кольце расположен заряд . В точке А он создает поле с потенциалом

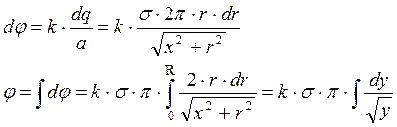
где сделана замена:  

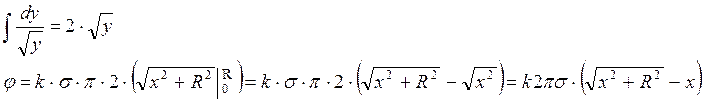
Из симметрии задачи следует, что напряженность поля пластинки в точке А будет направлена по оси х.

Учитывая связь между напряженностью и потенциалом , будем искать Е как

Задача №2

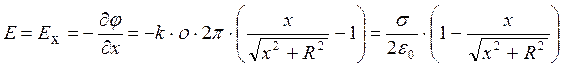
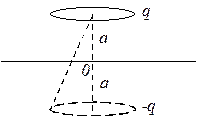
Тонкое проволочное кольцо радиуса R имеет заряд q. Кольцо расположено параллельно безграничной проводящей плоскости на расстоянии а от нее. Найти потенциал в центре кольца и поверхностную плотность заряда в точке плоскости, расположенной симметрично относительно кольца.

Решение

«Зарядом-изображением» будет кольцо зарядом –q, расположенное на расстоянии а по другую сторону плоскости. Поле в полупространстве, содержащем заданное кольцо, будет определяться этим кольцом и его «изображением».

Найдем потенциал системы зарядов:

Разобьем данный интеграл на 2:

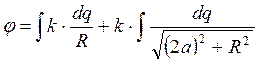  – для элементарных зарядов первого и второго колец.

Чтобы найти поверхностную плотность зарядов на плоскости в точке О, найдем там напряженность поля, которая у поверхности проводника определяется:

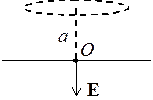Поле в точке О складывается из поля кольца заряда q и его «изображения». Эти поля одинаковы по величине и направлены в одну сторону. Таким образом,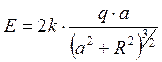

(см. задачу 2 из урока 1).

Направление напряженности поля у поверхности проводника в точке О указывает на отрицательный знак поверхностной плотности индуцированного заряда. Ее величина найдется как

Задача №3

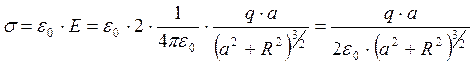
Точечный заряд q находится на расстоянии l от безграничной проводящей плоскости. Найти работу, которую совершит электрическая сила, действующая на заряд q при его медленном удалении на очень большое расстояние от плоскости.

Решение

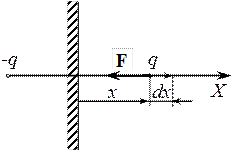По определению работа этой силы при элементарном перемещении dx:

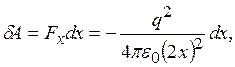
где выражение для силы получено с помощью метода изображений. Проинтегрировав это уравнение по x от l до ¥, найдем

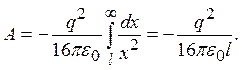
Замечание. Попытка решить эту задачу другим способом – через потенциал – приводит к неверному результату. Это связано с тем, что соотношение  справедливо только для потенциального поля. В системе же отсчета, связанной с проводящей плоскостью, электрическое поле индуцированных зарядов не потенциально: перемещение заряда q приводит к изменению распределения индуцированных зарядов, и их поле оказывается зависящим от времени.

Задача №4