Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле, страница 4

Система состоит из двух концентрических проводящих сфер, причем на внутренней сфере радиусом R₁ находится заряд q₁. Какой заряд q₂ следует поместить на внешнюю сферу радиусом R₂, чтобы потенциал внутренней сферы стал равным нулю? Как будет зависеть при этом потенциал j от расстояния r до центра системы?

Решение

Запишем выражения для потенциала вне системы (j_II) и в области между сферами (j_I):

,     , где j₀ – некоторая постоянная. Ее значение легко найти из граничного условия: при r = R₂ потенциал j_II = j_I. Отсюда

.

Из условия j_I (R₁)= 0 находим

               .

Зависимость j (r) будет иметь вид:

          

Урок №3

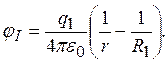
Электрическое поле в диэлектрике. Энергия электрического поля

Поле в диэлектрике является суперпозицией поля E₀ сторонних зарядов (q) и поля  связанных (поляризованных) зарядов (q’):

Поляризованностью диэлектрика называется суммарный дипольный момент единицы объема:

Для большинства диэлектриков, P= æ^.e₀^.E,       æ – диэлектрическая восприимчивость.

Поток вектора P через замкнутую поверхность, равен связанному заряду, находящемуся в объеме, ограниченном этой поверхностью, взятому с обратным знаком:

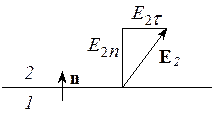
На границе раздела двух диэлектриков:

,

s¢ – поверхностная плотность связанных зарядов.

В диэлектрике теорема Гаусса для вектора E будет такой:

, т.е. следует учитывать все заряды – и сторонние, и связанные, охватываемые поверхностью S. Это неудобно, поэтому вводят вспомогательный вектор:

Как нетрудно убедиться, поток вектора D через замкнутую поверхность определяется только сторонними зарядами:

Для изотропных диэлектриков:

P= æ^.e₀^.E      и       D=e₀^.E +æ^.e₀^.E = (1+ æ)^.e₀^.E = e^.e₀^.E

где e – диэлектрическая проницаемость вещества.

Граничные условия:

, где s – поверхностная плотность сторонних зарядов

Энергия взаимодействия системы точечных зарядов: , где j_i – потенциал поля, создаваемого всеми остальными зарядами (кроме q_i) в точке, где расположен заряд q_i.

Если рассмотреть уединенный проводник, то энергия взаимодействия зарядов проводника между собой даст нам собственную энергию проводника:

,   где   – емкость проводника

При подсчете полной энергии системы следует учитывать собственную энергию всех зарядов и энергию их взаимодействия.

Оказывается, что энергию системы зарядов можно выразить через напряженность электрического поля, создаваемого этими зарядами. Объемную плотность электрической энергии можно найти по формуле:

.

Энергию электрического поля в некотором объеме V можно найти так:

.

Если интеграл взять по всему объему, где существует электрическое поле системы зарядов, то получим полную энергию этой системы.

Рассмотрим систему двух заряженных тел в вакууме (e= 1). Результирующее поле: .

Полная энергия этой системы найдется:

, где интегрирование ведется по всему пространству.

Понятно, что первое и второе слагаемые дают собственную энергию первого и второго проводников соответственно, а третье – энергию их взаимодействия.

Работа сил электростатического поля, как поля потенциальных сил, может быть найдена как убыль энергии: .

Энергия заряженного конденсатора: .

В плоском конденсаторе однородное электрическое поле локализовано только между его обкладками, поэтому .

Примеры решения задач

Задача №1

Первоначально пространство между обкладками плоского конденсатора заполнено воздухом, и 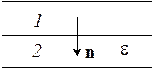напряженность поля в зазоре равна Е₀. Затем половину зазора, как показано на рисунке, заполнили однородным изотропным диэлектриком с проницаемостью e. Найти модули векторов E и D в обеих частях зазора, если при введении диэлектрика напряжение между обкладками не менялось.

Решение

До введения диэлектрика напряжение между обкладками:

, т.к. поле однородное, d – расстояние между обкладками.