Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле

Урок №1

Закон Кулона. Принцип суперпозиции. Теорема Гаусса.

Одно из фундаментальных взаимодействий – взаимодействие между электрическими зарядами.

Свойства электрического заряда:

1.  Существует в двух видах: положительный и отрицательный.

2.  В электрически изолированной системе суммарный заряд сохраняется.

3.  Величина заряда инвариантна по отношению к инерциальным системам отсчета.

4.  Величина заряда диэлектрика: q = N^.e, N– целое число, e = - 1.6^.10^-19 Кл.

Закон Кулона.

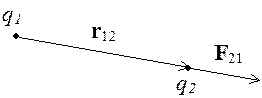Два точечных покоящихся заряда в вакууме взаимодействуют с силой , где r – расстояние между зарядами.

Сила направлена по прямой, соединяющей заряды, и является силой отталкивания, если заряды одноименные, и силой притяжения, если заряды разного знака.

                

     – в системе СИ       

     – электрическая постоянная

Законом Кулона можно воспользоваться и в том случае, если один из зарядов или оба заряда не являются точечными, но их распределение обладает сферической симметрией. В этом случае r – расстояние между центрами зарядов.

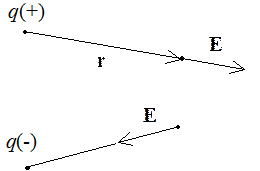Взаимодействие между зарядами осуществляется через поле, которое создается зарядом в окружающем пространстве.

  – напряженность поля, создаваемого зарядом q₁ в точке, определяемой радиус-вектором  

Отвлекаясь от индексов 1 и 2, .

Таким образом, напряженность поля в некоторой точке – это сила, действующая на единичный положительный заряд, помещенный в данную точку поля.

Принцип суперпозиции: напряженность электрического поля в данной точке определяется векторной суммой напряженностей полей, создаваемых отдельными зарядами в этой точке.

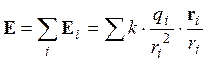
Если заряды распределены непрерывно, то

, где dq = t^.dl, t – линейная плотность заряда, или

dq = s^.dl, s – поверхностная плотность заряда, или

dq = r^.dV, r – объемная плотность заряда.

Силу, действующую на произвольный заряд q, помещенный в точку поля, где напряженность Е, можно найти по формуле:

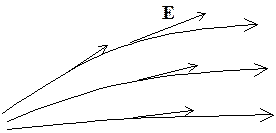Силовыми линиями электрического поля называются воображаемые кривые, в каждой точке которых вектор Е направлен к ним по касательной. Величину поля Е договоримся определять густотой силовых линий, т.е. количеством силовых линий, пересекающих единичную площадку к ним перпендикулярную.

Потоком вектора Е через площадку dS называется:

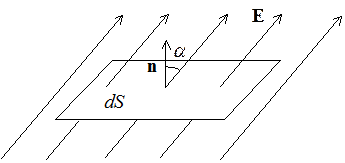Вектором площадки называется

где n – единичный вектор нормали к данной площадке. Если площадка замкнутая, то в качестве положительной нормали всегда выбирается внешняя.

Поток вектора Е через произвольную площадку S определяется:

Оказывается, что поток вектора Е через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на e₀:

Данное утверждение называют теоремой Гаусса.

Теорема Гаусса в дифференциальном виде:

, где

r – объемная плотность электрического заряда в той точке, где ищется .

Примеры решения задач

Задача №1

Тонкое полукольцо радиусом 10 см равномерно заряжено с линейной плотностью заряда 1 мкКл/м. В центре кривизны полукольца находится точечный заряд 20 нКл. Найти силу взаимодействия точечного заряда и полукольца.

Решение

Поскольку заряженное полукольцо не является точечным зарядом, то его следует мысленно разбить на элементарные заряды dq = t^.dl, где элемент дуги .

Сила взаимодействия dF между точечным зарядом q и элементарным зарядом кольца dq найдется по закону Кулона:

Результирующая сила F найдется векторной суммой всех dF, действующих на заряд q:

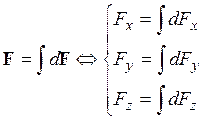
Из симметрии задачи можно понять, что результирующая сила F направлена вертикально вниз. Выберем в этом направлении ось y, тогда для величины силы F:

Задача №2

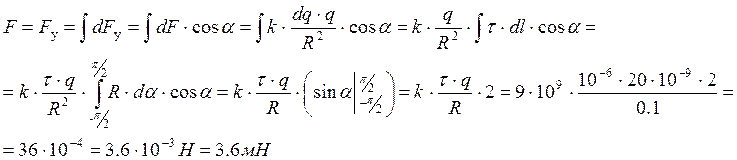
По тонкому кольцу радиуса 10 см равномерно распределен заряд 2 мкКл. Найти максимальную силу, действующую на точечный заряд 1 мкКл, находящийся на оси кольца.

Решение

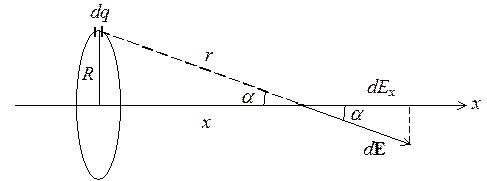Рассчитаем силу, действующую на заряд q₂, по формуле

, где E – напряженность поля, создаваемого кольцом.

Вычислим  по принципу суперпозиции. Мысленно разобьем кольцо на элементарные заряды dq, которые создают на оси кольца поле

Из симметрии задачи следует, что результирующий вектор E будет направлен по оси х, поэтому

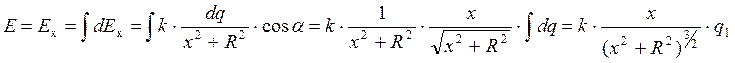
Суммирование всех элементарных зарядов по кольцу даст нам суммарный заряд кольца:

Таким образом,

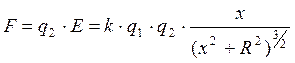
Чтобы найти максимальную силу, нужно определить расстояние х (от центра кольца до точки расположения заряда q₂), при котором функция F(x) имеет максимум:

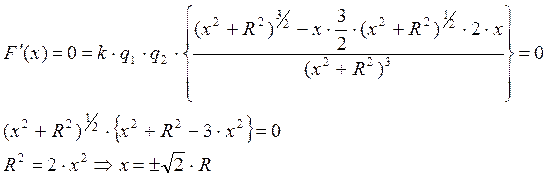
В двух точках на оси, расположенных слева и справа от плоскости кольца на расстоянии  от его центра, сила будет максимальной:

Задача №3

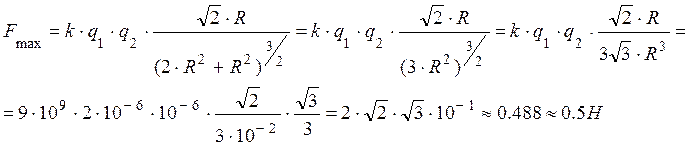
Две длинные прямые параллельные нити, заряженные равномерно с линейной плотностью 20 нКл/м, находятся на расстоянии 10 см. Найти напряженность поля в точке, лежащей на расстоянии 10 см от обеих нитей.

Решение

Поле E найдем по принципу суперпозиции, как сумму полей двух нитей: .

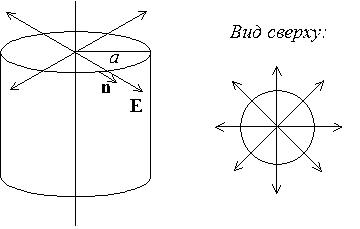Поле бесконечной нити на расстоянии «а» от нее найдем, используя теорему Гаусса. Из соображений симметрии задачи следует, что силовыми линиями являются радиально расходящиеся прямые, лежащие в плоскости, перпендикулярной нити.