Закон Кулона. Принцип суперпозиции. Теорема Гаусса. Потенциал. Проводник в электростатическом поле, страница 2

В качестве замкнутой гауссовой поверхности выберем цилиндр радиуса а, проходящий через интересующую нас точку (в которой нужно найти поле). Ось цилиндра совпадает с нитью. Посчитаем поток вектора E через замкнутую поверхность цилиндра:

Искомый интеграл по замкнутой поверхности цилиндра разобьем на 2:

, т.к. нормаль, проведенная к основаниям цилиндра, перпендикулярна силовым линиям.

Нормаль к боковой поверхности цилиндра в точке будет сонаправлена с силовыми линиями, поэтому . Учтем, кроме того, что величина напряженности во всех точках, одинаково удаленных от нити (т.е. на боковой поверхности цилиндра), будет одинакова. Тогда:

, где а – радиус цилиндра, h – его высота.

Итак,

По теореме Гаусса этот поток должен быть равен заряду, находящемуся внутри выбранного цилиндра, деленному на e₀. Внутри цилиндра расположен заряд участка нити длиной h: q = t^.h, где t – линейная плотность заряда нити.

Таким образом,

 

– напряженность поля бесконечной нити, заряженной с линейной плотностью t, на расстоянии «а» от нее.

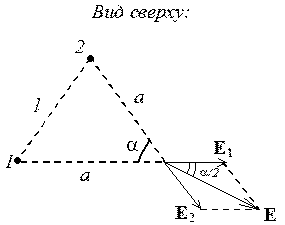Точками 1 и 2 обозначены бесконечно заряженные нити, перпендикулярные плоскости рисунка, E₁ и E₂ – напряженности полей, создаваемых этими нитями.

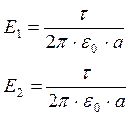
Поскольку а = l = 10 см, то в равностороннем треугольнике a = 60°.

Т.к. Е₁ = Е₂, то построенный на этих векторах параллелограмм для нахождения их векторной суммы является ромбом, и

Задача №4

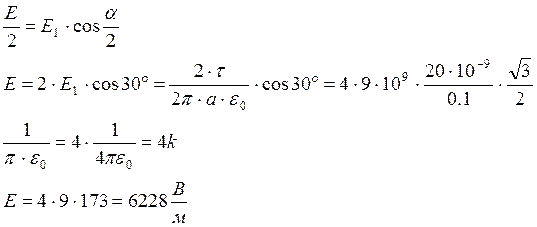
Найти напряженность электрического поля распределенного заряда, объемная плотность которого обратно пропорциональна квадрату расстояния до точки О: .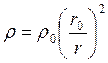

Решение

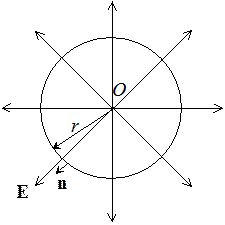Из сферически симметричного распределения заряда следует, что силовыми линиями поля будут радиально расходящиеся прямые из точки О. В связи с этим, в качестве замкнутой поверхности для теоремы Гаусса выберем сферу радиуса r с центром в точке О.

В каждой точке поверхности сферы вектор E и нормаль к поверхности будут сонаправлены, поэтому . Кроме того величина напряженности Е всюду на одинаковом расстоянии от точки О (т.е. на поверхности выбранной сферы) будет одинаковой. Таким образом,

Чтобы применить теорему Гаусса, нужно посчитать суммарный заряд, расположенный внутри этой сферической поверхности:

, т.к. плотность заряда зависит от r, в качестве dV выберем узкий сферический слой: 

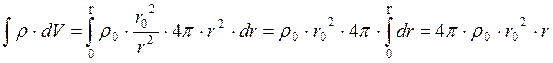
Учитывая, что :

Урок №2

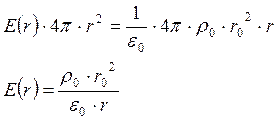
Потенциал. Проводник в электростатическом поле

Электростатическое поле является потенциальным. Работа сил такого поля по замкнутому контуру равна 0:

Каждой точке поля можно поставить в соответствие потенциал j – энергию единичного положительного заряда. Тогда энергия любого заряда, помещенного в данную точку поля .

Разность потенциалов между любыми двумя точками:

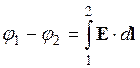, где контурный интеграл берется по любому пути от точки 1 до точки 2.

Кроме того, напряженность можно найти как

Потенциал поля точечного заряда на расстоянии r от него: .

Знак потенциала совпадает со знаком заряда q.

Потенциал поля системы зарядов равен сумме потенциалов полей отдельных зарядов в заданной точке:

Если заряды распределены непрерывно:

Работа сил электростатического поля по переносу заряда q из точки 1 в точку 2 ищется, как убыль потенциальной энергии:

 

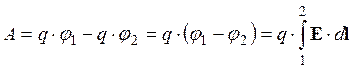
Эквипотенциальной поверхностью называется геометрическое место точек, потенциалы которых одинаковы. Силовые линии перпендикулярны эквипотенциальным поверхностям и направлены в сторону уменьшения потенциала.

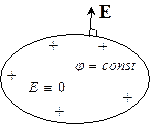Объем заряженного проводника является эквипотенциальным, поэтому заряженный проводник характеризуют величиной потенциала. Отношение  называется емкостью уединенного проводника.

Напряженность поля вблизи поверхности проводника равна:

  и перпендикулярна поверхности.

Так, потенциал заряженного сферического проводника радиуса R равен: