Построение математической модели объекта управления в пространстве состояния. Структурная схема объекта управления

Часть 1.

Задание 1. По виду электрической схемы построить математическую модель объекта управления в пространстве состояния.

Задание 2. По построенной модели составить структурную схему и сигнальный граф.

Задание 3. Используя формулу Мэйсона найти передаточную объекта управления.

Задание 4. По передаточной функции объекта управления определить временные и частотные характеристики и построить их зависимость.

Задание 5. По полученным зависимостям определить прямые и косвенные оценки качества ОУ.

Часть 2.

Задание 1. По заданной корреляционной функции К_x(τ) определить спектральную плотность S_x(ω) для белого шума, который подаётся на вход формирующего фильтра.

Задание 2. По заданным статическим характеристикам S_E и S_V определить передаточную функцию формирующего фильтра ψ(р).

y(t)

x(t)

V(t)

Ψ(р)

W(p)

Задание 3. Представить объект управления в виде:

и оценить качество полученной системы по переходной характеристике.

Задание 4. Сделать вывод по работе.

Дано:

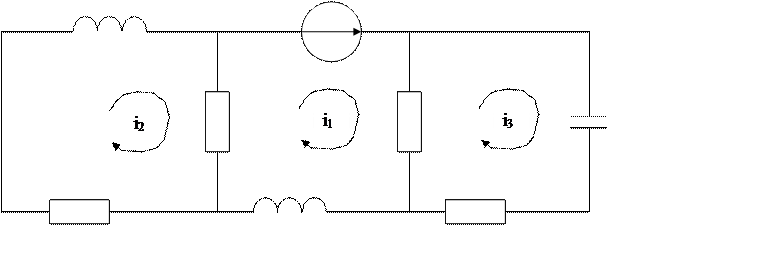                          L₁                                          e(t)

R₁                                      R₂                                                                                                                   C₂  

R₃                                                                L₃                                               R₄

R₁ = 343 Ом

R₂ = 435 Ом

R₃ = 151 Ом

R₄ = 204 Ом

L₁ = 20 Гн

L₃ = 48 Гн

С₂ = 21421*10 ^{- 6} Ф

Входной сигнал e(t). Выходной сигнал i₃.

Часть 1.

i3

e(t)

ОУ

1. Постоим математическую модель объекта управления в пространстве состояния. Структурная схема объекта управления:

В схеме три элемента, запасающих энергию L₁, L₃, C₂ следовательно математическая модель должна быть третьего порядка.

2. Построение математической модели:

а) зададимся направлением контурных токов i₁, i₂, i₃. Составляем три уравнения по второму закону Кирхгофа для контуров:

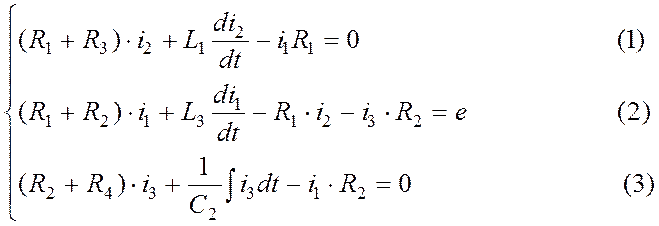
В уравнении (3) есть интеграл, поэтому дифференцируем его:

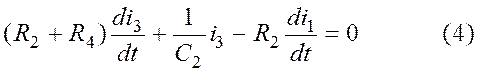
Уравнения (4) содержит производную второго порядка и в качестве х₁ выбираем элементы с производными, производные берём на порядок ниже:

Введём х₂ и х₃ по тому же принципу:

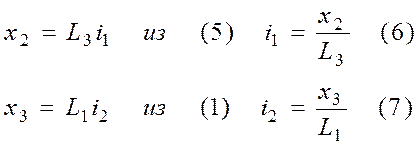
Запишем введённый вектор состояния в виде дифференциальных уравнений первого порядка:

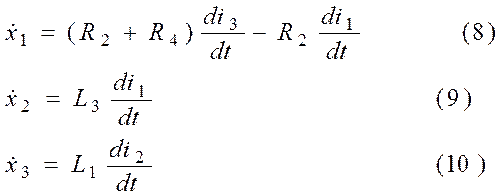
Правые части этих уравнений находятся в (4), (5), (1). Вынесем эти элементы в данных выражениях в левые части и заменим производными вектора состояния. Тогда из (4), (5), (1)и с учётом (8), (9), (10) запишем:

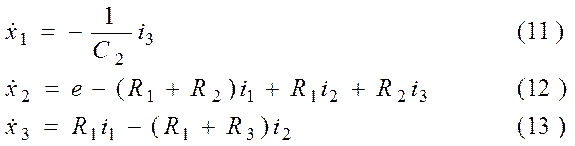
Из уравнения (5) следует:

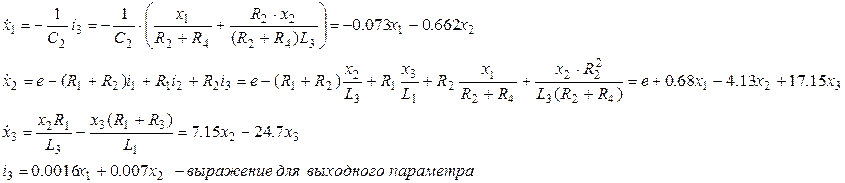
Получили 3 дифференциальных уравнения и одно уравнение для выходного параметра. Запишем полученную систему уравнений в матричном виде:

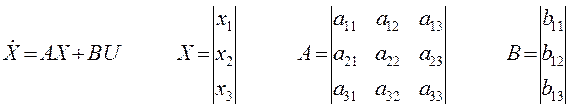
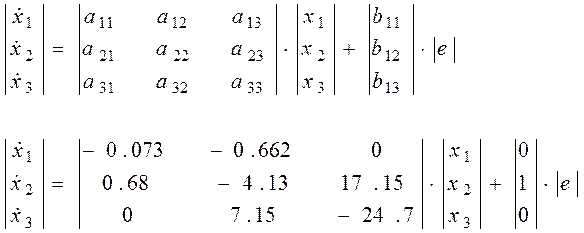
Получим матричное уравнение для выходной переменной:

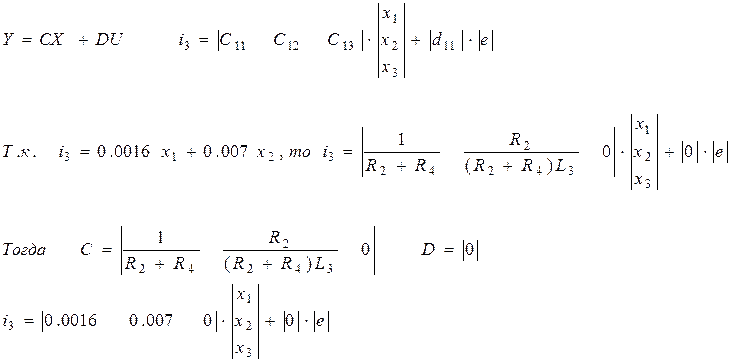
3. Построение сигнального графа и структурной схемы системы.

Перепишем уравнения в общем виде для построения графа системы:

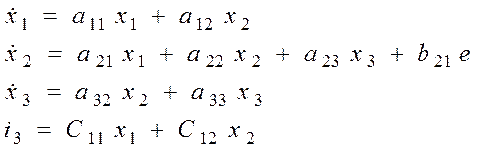
Построение графа.

 

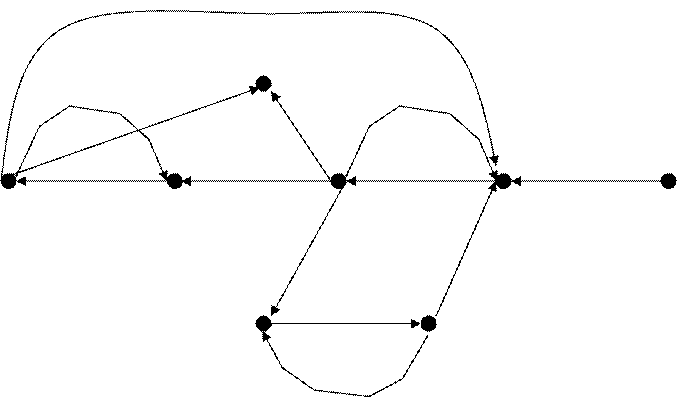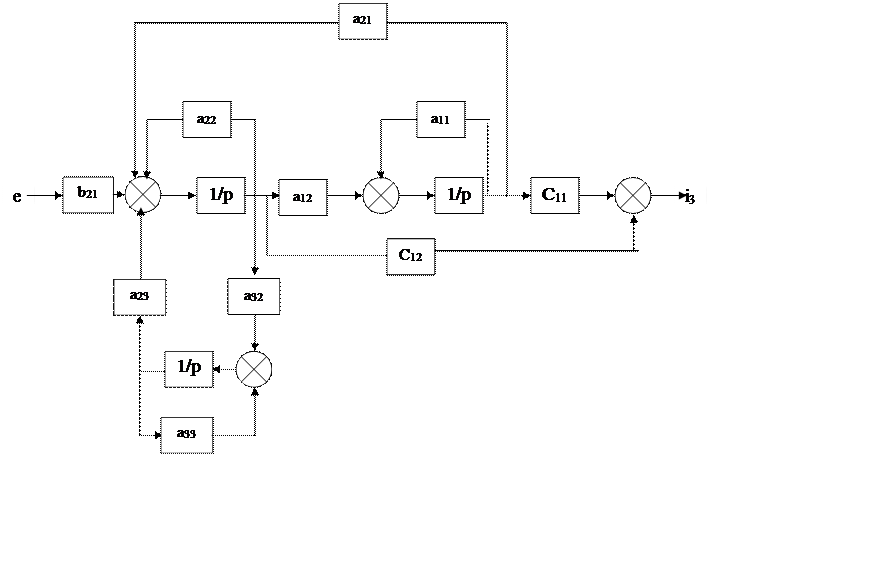Построим структурную схему:

4. Найдём передаточную функцию по Формуле Мэйсона.

1) В данном случае есть 2 пути от входа к выходу:

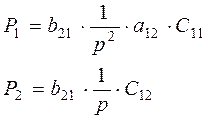
2) В системе имеется 5 замкнутых контуров:

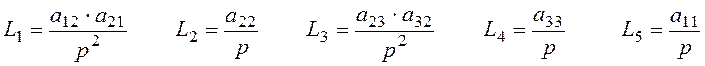
3) Определитель системы включает 5 контуров и пять пар некасающихся контуров:

Δ = 1 – L₁ – L₂ – L₃ – L₄ – L₅+ L₄L₂ + L₄L₁+ L₄L₅+ L₃L₅+ L₂L₅

4) Количество сомножителей равно количеству прямых путей. Выражение для Δ_i записывается как выражение для Δ, не разрываются контуры, через которые проходит прямой путь Р_i

Сомножитель для первого пути Р₁. При размыкании этого пути размыкаются 4 контура, кроме L₄:    Δ₁ = 1 – L₄

Сомножитель для второго пути Р₁. При размыкании этого пути размыкаются 3 контура, кроме L₄ и L₅:    Δ₂ = 1 – L₄ – L₅

5) Запишем и преобразуем выражение передаточной функции:

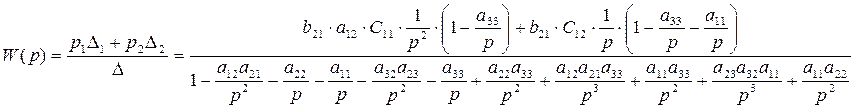
После подстановки значений коэффициентов и преобразований