МОДЕЛИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ
1. СПОСОБЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ IIIПРЕРЫВНЫХ СИСТЕМ
Omei. При математическом описании непрерывных систем исполь-Пимен: I .Дифференциальные уравнения. 2.Передаточные функции
(_вязь между входом х и выходом у в общем виде в непрерывной системе имеет вид:
![]()
||„, аь...bo - постоянные коэффициенты, характеризующие параметры шена; bo, Ьь...Ьц - постоянные коэффициенты, определяющие параметры управляющего сигнала.
Передаточная функция может быть записана в четырех формах:
I .Операторная.
2. Стандартная.
3.Форма изображений по Лапласу.
4, Частотная.
Передаточная функция в операторной форме:
![]()
где D(p) - собственный оператор; М(р) - оператор воздействия; р — оператор дифференцирования.
Стандартная форма передаточной функции:
|
|
где k -коэффициент передачи, ТЧюстоянные времени. В форме изображений по Лапласу:
|
|
|
|
где U(to) - действительная часть; V(to) - мнимая; А{ео)- амплитудно-частотная характеристика; qKa) - фазо-частотная характеристика.
|
|
2. СПОСОБЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ДИСКРЕТНЫХ СИСТЕМ
Ответ. При .математическом описании дискретных систем исполь зуются: ,
1. Конечно-разностные уравнения.
2. Преобразование Лапласа. ,
3. Z-преобразования.
Связь между входом х и выходом у в общем виде в дискретной системе имеет вид:

,1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МНОГОМЕРНЫХ ОМ.ККТОВ
Umri, ( ЛУ может содержать элементы с несколькими входными и (.i.c.(iinii,iMii «дичинами. Такие системы называются многомерными. Мри иц мшсматическом описании патучают систему дифференциальмыи у|шннсиий, в правые части которой входят несколько функций •|и»мгии. Количество уравнений равно количеству выходных перемен ных. Эта система дифференциальных уравнений тт математическое описание многомерной системы или объекта. .- : .
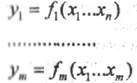
При векторной форме описания систем используем переменные: нсктор входа (вектор входных величин, сигналов);вектор выхода (вектор выходных величин, сигналов );вектор состояния (вектор переходных состояний ).
Тогда математическое описание системы будет состоять яз векторного дифференциального уравнения состояние, и ,алгебраического уравнения выхода
|
|
|
При описании элементов дискретного действия в общем виде получим разностные уравнения: |
|
|
|
Передаточная матрица многомерной системы имеет вид: |
Для непрерывных систем: , - ;•..- .'.-., ,-<
4, МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОБЪЕКТОВ ИЛИ
СИСТЕМ С ПОМОЩЬЮ ГРАФОВ
Ответ. Граф можно составить по дифференциальному уравнению, разностному уравнению, записанным с использованием изображения функций или с помощью передаточной функции, записанной в р - или
z -^ формах. При этом можно оценить влияние параметров уравнений или звеньев в связей между ними на динамические характеристики элементов. В результате можно упростить структуру элемента, определить в нем сильные и слабые связи. Исключая слабые связи можно провести операции декомпозиции.
Граф - пара множеств: точек (вершин), дуг (ветвей), соединяющих точки.
Графы, дуга которых имеют направление, называются ориентированными, а графы, не имеющие направления - неориентированные. Графы, дугам которых приписаны некоторые веса, называются взвешенными, а графы, не имеющие весов - невзвешенные.
При составлении графов, соответствующих заданным структурным схемам каждая вершина определяет некоторый сигнал системы, дуга -переход» вес дуги соответствует передаточной функции элемента.
Оптимизация неориентированного графа заключается в определении минимального покрывающего дерева. Минимальное покрывающее дерево - дерево величина которого минимальна. Дерево графа - совокупность ветвей или дуг, которые соединяют
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.