Выбор оптимальной схемы доставки грузов. Метод северо-западного угла. План двойного предпочтения. Метод Фогеля, страница 7

Проверяем план по строкам:

1стр. 9 = 2,5+0,5+2.4 = 5,4 (ед);

2стр. 3 = 2.4+0,6 (ед);

3стр. 7 = 1.9+1,8+1,1+2,2 (ед).

Первый тип механизации используется не полностью. Неиспользованное количество механизации 4,6 ед. выводится в резерв.

Проверяем план по столбцам:

1ст. 150 = 2,4*62 = 148,8 т.т.;

2ст. 210 = 2,5*47+1,9*49 = 210,6 т.т.;

3ст. 110 = 1,8*62= 111,6 т.т.;

4ст. 60 = 0,5*49+0.6*61 = 61,1 т.т.;

5ст. 110 = 2,4*46 = 110 т.т.;

6ст. 70 = 1,1*62 = 68,2 т.т.;

7ст. 120 = 2.2*54 = 118,8 т.т.

Определяем функцию цели:

F = 2,5*19+0,5*17,8+2,4*18+2.4*25.4+0,6*25,9+1,9*15+14,7*1,8+

+1,1*15,1+2,2*15=280,67 млн.руб.

Вывод: после составления трех планов разными методами и сравнения функций целей выяснил, что по методу разницы себестоимости функция цели получила меньшее значение.

2.5.  Метод потенциалов.

План считается оптимальным, если выполняется условие для базисных клеток

α_i + β_j П_ij= Э_ij

для свободных клеток

α_i + β_j П_ij≤ Э_ij

где   α_i + β_j  - соответственно потенциалы строк и столбцов.

Принимаем α₁=0.

Алгоритм решения методом потенциалов:

1.  В первоначальный допустимый план водятся дополнительные строки и столбцы (таблица 12);

2.  Рассчитываются потэнцыалы строк и столбцов из условия

α_i + β_j П_ij= Э_ij

3.  Рассчитывается потенциал свободных клеток из условия

α_i + β_j П_ij≤ Э_ij

4.  Если условие не выполняется то строится контур переноса ресурсов;

5.  План проверяется на невырождаемость

Б.к. = m + n -1

6.       План проверяется на ограничения;

7.       Определяется функция цели:

         

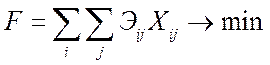Расчет потенциала базисных клеток:

1;2   α₁ + β₂ П₁₂ = Э_1;2 ,   0 + β₂*47 = 19,    β₂ = 0,4;

1;4   α₁ + β₄ П₁₄ = Э_1;4 ,   0 + β₄*49 = 17,8,    β₄ = 0,36;

1;5   α₁ + β₅ П₁₅ = C_1;5 ,   0 + β₅*46 = 18,    β₅ = 0,39;

1;7   α₁ + β₇ П₁₇ = C_1;7 ,   0 + β₅*49 = 19,    β₇ = 0,39;

2;7   α₂ + β₇ П₂₇ = C_2;7 ,   α₂ + 0,39*60 = 26,4,    α₂=3;

3;2   α₃ + β₂ П₃₂ = C_3;2 ,   α₃ + 0,4*49 = 15,   α₃ = -4,6;

3;1   α₃ + β₁ П₃₁= C_3;1,   -4,6 + β₁ *48 = 14,4,   β₁  = 0,4;

3;3   α₃ + β₃П₃₃ = C_3;3,   -4,6+ β₃*62 = 14,7 β₃ = 0,31;

3;6   α₃ + β₆П₃₆ = C_3;6,   -4,6+ β₆*62 = 15,1,   β₆ = 0,32.

Таблица 12

Расчет потенциала свободных клеток:

1;1  α₁ + β₁ П₁₁≤ C_1;1        0 + 0,4*46 ≤ 18,4   (“-“);     

1;3  α₁ + β₃ П₁₃≤ C_1;3        0 + 0,31*48 ≤ 17,9 (“-“);     

1;6  α₁ + β₆ П₁₆≤ C_1;6        0 + 0,32*45 ≤ 18,5 (“-“);     

2;1  α₂ + β₁ П₂₁≤ C_2;1        3 + 0,4*62 ≤ 25,4 (“+“);

2;2  α₂ + β₂ П₂₂≤ C_2;2        3 + 0,4*53 ≤ 26,2 (“-“);

2;3  α₂ + β₃ П₂₃≤ C_2;3        3 + 0,31*64 ≤ 26,4 (“-“);

2;4  α₂ + β₄ П₂₄≤ C_2;4        3 + 0,36*61 ≤ 25,9 (“+“);          

2;5  α₂ + β₅ П₂₅≤ C_2;5        3 + 0,39*52 ≤ 27 (“-“);     

2;6  α₂ + β₆ П₂₆≤ C_2;6        3 + 0,32*59 ≤ 23,3 (“-“);     

3;4  α₃ + β₄ П₃₄≤ C_3;4        -4,6+ 0,36*40 ≤ 14,8 (“-“);

3;5  α₃ + β₅ П₃₅≤ C_3;5        -4,6+ 0,39*51 ≤ 14,6 (“+“);     

3;7  α₃ + β₇ П₃₇≤ C_3;7        -4,6+ 0,39*54 ≤ 15   (“+“);     

В полученном плане условие α_i + β_jП_ij≤ Э_ij  не выполняется,  строится контур переноса ресурсов (таблица 12). Перераспределяем ресурсы (таблица 13).

3;1  Х₃₁  = min{ 7-1,8-1,1; ^150-0,4*62/₄₈} = 2,6 ед;

3;2  Х₃₂ = min{1,5; ²¹⁰/₄₉} = 1,5 ед;

1;2  Х₁₂ = min{ 9-1,2-2,4; ^210-1,5*49/₄₇} = 2,9 ед;

1;7  Х₁₇ = min{ 5,4-2,9; ¹²⁰/₄₉} = 2,4 ед;