Выбор оптимальной схемы доставки грузов. Метод северо-западного угла. План двойного предпочтения. Метод Фогеля, страница 4

5.  План проверяется на невырождаемость

Б.к. = m + n -1

4.       План проверяется на ограничения;

5.       Определяется функция цели:

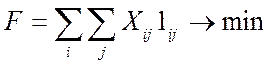Таблица 5      (Метод потенциалов)

Пункт отправления	Gi	αi	Пункт назначения
			В1		В2		В3		В4		Вф
			Gj
			60		110		70		120		110
			βj
			14		12		9		10		100
A1	150	0		“-“		“-“		“-“	120		30
				21		51		27		10		100
A2	210	0		“-“	110		70			“-“	30
				47		12		9		17		100
A3	110	0	60			“-“		“-“		“-“	50
				14		15		19		12		100

Расчет потенциала базисных клеток:

1;4   α₁ + β₄ = C_1;4 ,   0 + β₄ =10,    β₄ = 10;

1;5   α₁ + β₅ = C_1;5 ,   0 + β₅ = 100,    β₅ = 100;

2;5   α₂ + β₅ = C_2;5 ,   α₂ + 100 = 100,   α₂ = 0;

2;3   α₂ + β₃ = C_2;3 ,   0 + β₃ = 9,    β₃ = 9;

2;2   α₂ + β₂ = C_2;2 ,   0 + β₂ = 12,   β₂  = 12;

3;5   α₃ + β₅ = C_3;5 ,   α₃ + 100 = 100,   α₃ = 0;

3;1   α₃ + β₁ = C_3;1 ,   0 + β₁ = 14,   β₁  = 14;

Расчет потенциала свободных клеток:

1;1  α₁ + β₁ ≤ C_1;1        0 + 14 ≤ 21   (“-“);      

1;2  α₁ + β₂ ≤ C_1;2        0 + 12 ≤ 51   (“-“);     

1;3  α₁ + β₃ ≤ C_1;3        0 + 9 ≤ 9   (“-“);     

2;1  α₂ + β₁ ≤ C_2;1        0 + 14 ≤ 47   (“-“);     

2;4  α₂ + β₄ ≤ C_2;4        0 + 10 ≤ 17   (“-“);     

3;2  α₃ + β₂ ≤ C_3;2        0+ 12 ≤ 15   (“-“);     

3;3  α₃ + β₃ ≤ C_3;3        0 + 9 ≤ 19   (“-“);     

3;4  α₃ + β₄ ≤ C_3;4        0 + 10 ≤ 12   (“-“);     

План, получился оптимальным, т.к. удовлетворяет условию базисных клеток α_i + β_j = C_ij и для свободных клеток α_i + β_j ≤ C_ij

1.6. Корреспонденция перевозок

Полученный оптимальный план взаимной увязки поставщиков и потребителей оформляем в виде корреспонденции перевозок местных грузов.

Таблица 6      (Корреспонденция перевозок)

Пункты		Масса перевозок тыс.т	Удельные транспортные затраты по перевозке, руб/т	Затраты тыс.руб
отправления	назначения
А5	В5	110	37	4070
А5	В6	45	22	990
А5	Вф	45	1000	45000
А6	В4	45	12	540
А6	В6	75	12	900
А7	В4	45	7	315
А7	В7	105	9	945
ИТОГО:		470		52760

II. Распределительная задача

         2.1. Исходные данные:

Содержание: расстановка имеющейся перегрузочной техники по пунктам обработки флота.

Необходимо найти такой вариант решения задачи, который обеспечивал бы экстремальное значение критерия оптимальности при следующих условиях:

а) на всех участках продолжительность навигации одинакова;