Gоп = 1,1*(22,848 + 603,0 + 298,75)*2,4 = 2440,939 тс;
Nвр = 1,1*1,0*14*(89,10 + 89,10)/2 = 1372,14 тс;
åN = 682,682 + 2440,939 + 1372,14 = 4495,761 тс
Gc = 1,1*2,4*(3,14*1,62/4)*25 = 132,7 тс
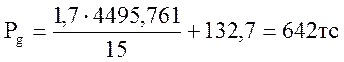
При применении 15 свай диаметром 1,6 м, длиной 25 несущая способность сваи по грунту составит Fd = 700 тс
642 тс < 700 тс Условие выполняется.
Принимаем 15 свай диаметром 1,6 м и длиной 25 м под опору.
Объемы работ и определение стоимостей конструктивных элементов моста приведены в таблице 5.
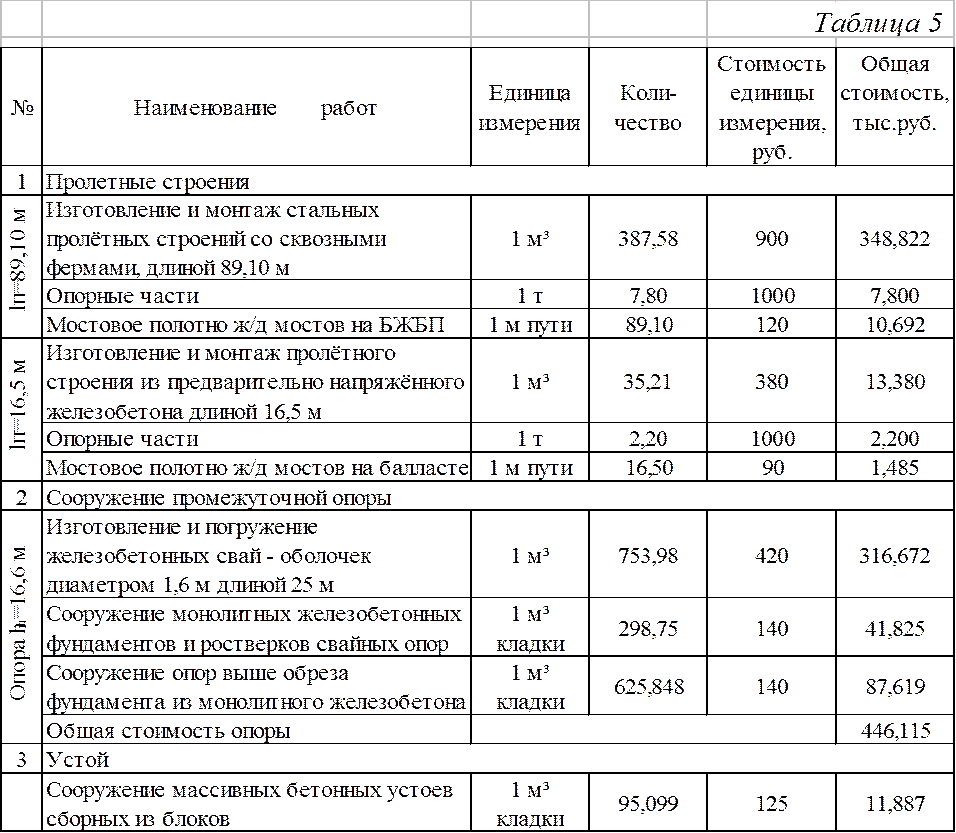
Определение общей стоимости моста приводится в таблице 6.
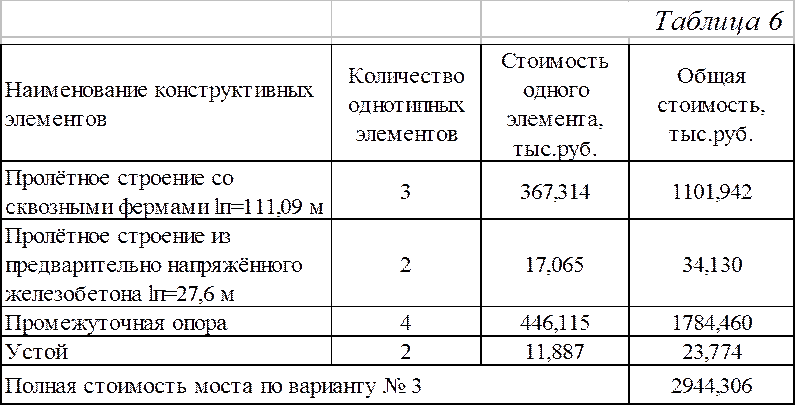
1.4 Сравнение вариантов.
Сопоставление капитальных затрат по вариантам приведено в таблице 7.
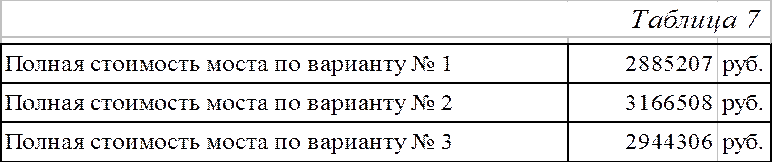
Самым экономичным по капитальным затратам оказался мост по первому варианту.
2. Расчет пролетного строения.
Проезжая часть пролетных строений работает в сложных условиях. Через мостовое полотно она непосредственно воспринимает местную нагрузку от подвижного состава и, связана с главными фермами, взаимодействует с ними и воспринимает дополнительные усилия от совместной работы с ездовыми поясами главных ферм.
Определим сначала усилия в продольных и поперечных балках, необходимые для их расчета на прочность.
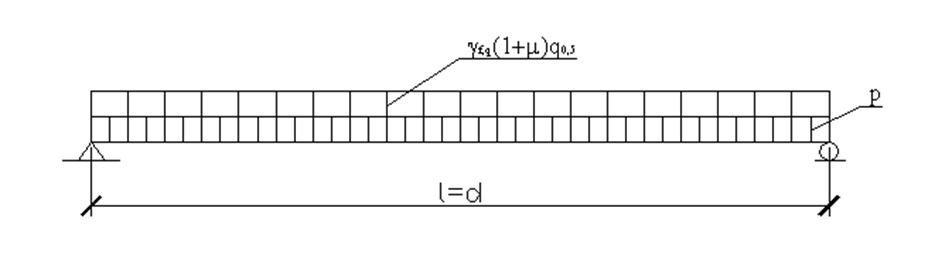
Рис. 2.1. Расчетная схема продольной балки.
Собственный вес двух продольных балок с учетом веса связей между балками можно ориентировочно определять по формуле:
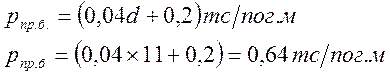
где d– панель продольной балки.
Расчетная постоянная нагрузка на одну балку при расчете на прочность будет равна:
где pмп – собственный вес мостового полотна. pмп=2,3 тс/м.
.
Находим эквивалентные нормативные временные нагрузки на продольные балки заданного класса q0.5 и q0, и коэффициенты к ним γ f,q и 1+μ.
γ f,q= 1,3--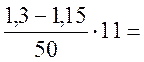
1,267.
1+μ=1+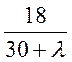
;
1+μ=1+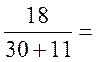
1,44.
q0.5 =21,39 тс/м; q0=24,44 тс/м;
Расчетные усилия в продольной балке при расчете на прочность определяют по
формулам.
Наибольший изгибающий момент в середине пролета:
М0,5=(p*d2)/8+0.5*γ f,q *(1+ μ)*( q0.5* d2)/8.
М0,5 =(1,73*112)/8+0,5*1,267*1,44*(21,39*112)/8=321,3 тс*м.
Наибольшая поперечная сила у опоры:
Q0=(p*d)/2+0.5*γ f,q *(1+ μ)*( q0* d)/2.
Q0=(1,73*11)/2+0,5*1,267*1,44*(24,44*11)/2=132,14 тс.
где q0.5, q0 – эквивалентная временная вертикальная нагрузка для линий влияния с параметрами λ=d и α, равными соответственно 0,5и 0;
0,5 – коэффициент, учитывающий распределение временной нагрузки на две продольные балки.
При расчете поперечной балки в качестве расчетной схемы можно принимать свободно опертую балку на двух опорах с пролетом, равным расстоянию между осями главных ферм B.
Поперечная балка воспринимает собственный вес и давления Д от продольных балок в смежных панелях. По сравнению с этими силами собственный вес поперечной балки невелик, и при эскизных расчетах им можно пренебречь.
Наибольший изгибающий момент в пролете на участке b при расчете на прочность:
где 
, w - площадь линии влияния Д.
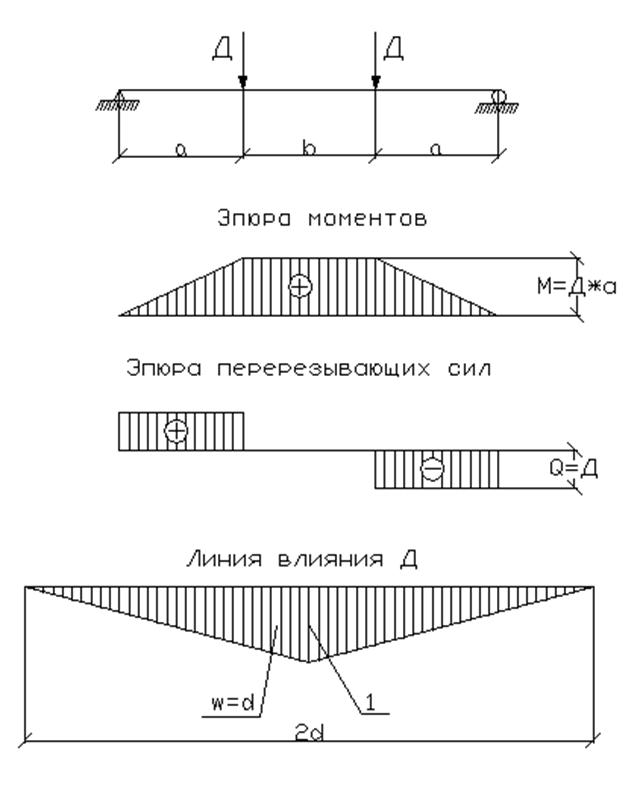
Значения γ f,q , 1+μ и q определяются для линий влияния при λ=2d и α=0,5.
Вычисляем значения γ f,q , 1+μ и q:
γ f,q= 1,3-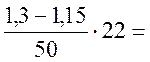
1,234;
1+μ=1+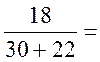
1,34;
q=17,98тс/м. b=1,7 м.
Определяем силовые воздействия Д на поперечную балку:
Д=1,73*11+0,5*1,234*1,34*17,98*11=182,55 тс.
Изгибающий момент и перерезывающая сила в поперечной балке соответственно равны:
М=182,55*2,05=374,22 тс*м. Q=182,55 тс.
Сечения балок принимаются двутавровыми. С целью обеспечения более простой и надежной конструкции прикрепления продольной и поперечной балок их высоты целесообразно принять одинаковыми. Материал пролетного строения сталь марки 15ХСНД, поставляемые в термоулучшенном состоянии. Расчетное сопротивление по пределу текучести 3000 кгс/см2 при толщине проката от 8 до 32 мм.
2.1.2.1 Подбор сечения продольной балки
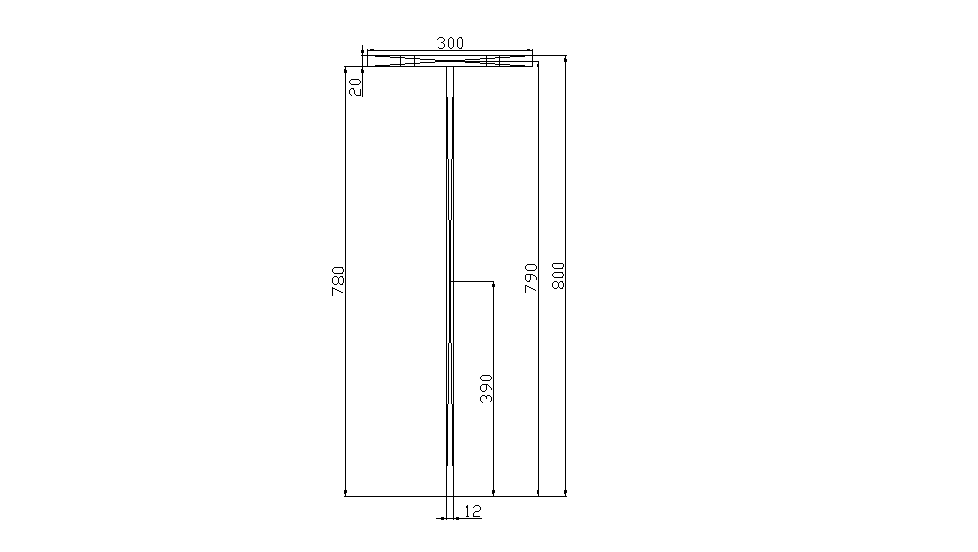
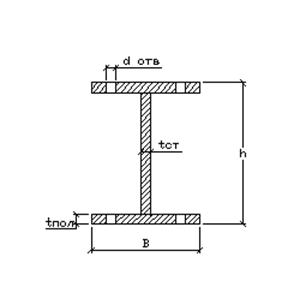Высоту балки назначаем h=1600 мм.
Размеры балки принимаем: В=300 мм
tст=12 мм
tпол=20 мм.
Принимаем высокопрочные болты диаметром dб=22 мм, тогда отверстие под болт принимаем диаметром d=25 мм.
Ix=2[(93,6*392)+(60*792)+(1,2*783)/12+(30*23)/12] =1128602 см4
∆I=4*[(2,5*23)/12+2,5*2*792] = 124827 см4
In= Ix-∆I=1128602-124827 = 1003775 см4
Wn= 2*In/h=2*1003775/160 = 12547,2 см3
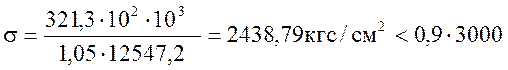
Проверка выполнена.
Проводим проверку по максимальным касательным напряжениям:
,
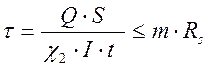=1,25-0,25*(τmin,ef/ τmax,ef),
где Q – перерезывающая сила
Q=132,14 тс;
τmin,ef/ τmax,ef-значения минимального и максимального напряжений в сечении стенки. Χ2-коэффициент, учитывающий неравномерность распределения в стенке касательных напряжений;
S– статический момент балки
S-8390,4 см4
I – момент инерции балки
I – 1128602 см4
tст – толщина листа стенки
tст=1,2 см;
Rs – расчетное сопротивление на сдвиг по пределу текучести
Rs=0.58·Ry;
S0.5 г.л=F2* y2. S0.5 г.л=60*79 =4740 см3
S0.5 в.л= F1* y1 S0.5 в.л=93,6*39=3650,4 см3
Sn= S0.5 г.л ∑S0.5 =8390,4 см3
τmin,ef=(Q*Sn)/(Jx*t)
τmin,ef=(132,14*4740*
)/(1128602*1,2) = 463,39
τmax,ef=(Q*∑S0.5)/(Jx*t)
τmax,ef=(132,14*8390,4*)/(1128602*1,2) = 818,64
=1,25-0,25*(463,39/818,64)=1,108
< 
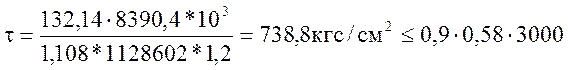
Проверка выполнена:
2.1.2.2. Подбор сечения поперечной балки
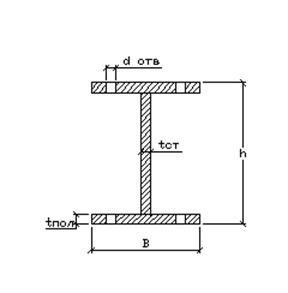
Высоту балки назначаем h=1600 мм.
Размеры балки принимаем: В=350 мм
tст=12 мм
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.