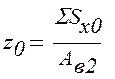
Где: ∑Sx0 – сумма статических моментов поясов и стенки, определяемая как сумма произведений площади сечения поясов и стенки на расстояние от центра тяжести пояса или стенки до оси х0 относительно которой определяется статический момент.
3) Момент инерции швеллера относительно оси х2 определяемый как сумма произведений площади сечения поясов и стенки на квадрат расстояния от центра тяжести пояса и стенки до оси х2 .
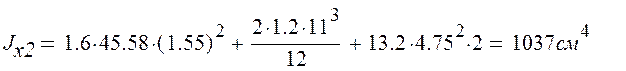
4) Момент инерции швеллера относительно оси у:
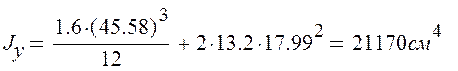
5) Радиусы инерции сечения:
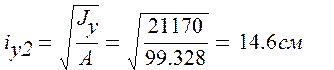
Уточняется положение центра тяжести сечения колонны:
- определяется расстояние между осями х1 и х2:
- определяется расстояние от оси х до оси х1:
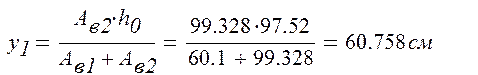
- определяется расстояние от оси х до оси х2:
Так как значения у1 и у2 отличаются от первоначально принятых значений, необходим перерасчет усилий в ветвях колонны.
Далее проводится проверка устойчивости ветвей колонны из плоскости рамы (т.е. относительно оси у-у), ly = 867см.
Вначале проводится проверка устойчивости подкрановой ветви по формуле:
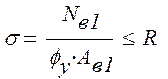
Где: φу – коэффициент продольного изгиба, определяемый интерполяцией в зависимости от гибкости ветви по (1, прил.7).
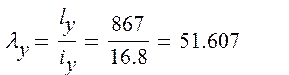
При R = 200 МПа:
При R = 240 МПа:
При R = 225МПа:
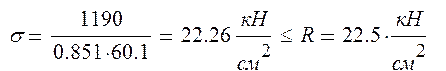
Устойчивость ветви обеспечивается.
Проводится проверка устойчивости наружной ветви по формуле:
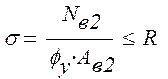
По (1, прил.7) определяется коэффициент продольного изгиба φу в зависимости от гибкости:
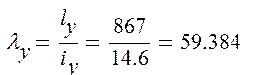
При R = 200 МПа:
При R = 240 МПа:
При R = 215МПа:
Устойчивость ветви обеспечивается.
Из условия равноустойчивости подкрановой ветви в плоскости рамы λх1 = λу определяется требуемое расстояние между узлами решётки lв1.
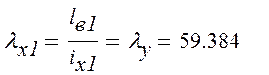
Отсюда:
Принимаем lв1 = 204 см, разделив нижнюю часть колонны на
чётное число панелей.
Проверяется устойчивость ветвей в плоскости рамы (относительно осей х1 - х1 и х2 - х2).
Для подкрановой ветви:
- определяется гибкость ветви:
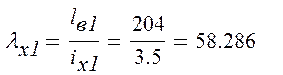
- определяется коэффициент продольного изгиба φх в зависимости от λх1 по (1, прил.7):
При R = 200 МПа:
При R = 240 МПа:
При R = 225МПа:
- проводится проверка устойчивости:
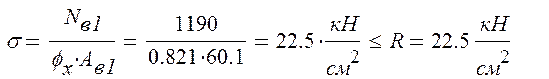
Для наружной ветви:
- определяется гибкость ветви:
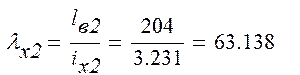
- определяется коэффициент продольного изгиба φх в зависимости от λх2 по (1, прил.7):
При R = 200 МПа:
При R = 240 МПа:
При R = 215МПа:
- проводится проверка устойчивости:
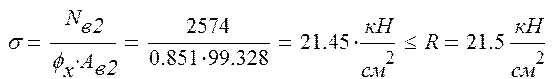
Устойчивость ветви в плоскости рамы обеспечивается.
4.5 Расчёт решётки подкрановой части колонны.
Максимальная поперечная сила, действующая в сечении колонны
(сечение 2-1) принимается из таблицы расчётных усилий по результатам статического расчёта рамы Qmax= 60.55 кН.
Условная поперечная сила, возникающая в колонне определяется по приближённой формуле Qусл ≈ 0.2·А, где А – площадь сечения нижней части колонны, Qусл ≈ 0.2·(60.1+107.2)= 33.46 кН.
Расчёт решётки производится по максимальной из двух, полученных расчётами поперечных сил, т.е. по Qmax= 60.55 кН.
Определяется усилие сжатия в раскосе:
Где: α – угол наклона раскоса к вертикали, sinα = hн/lp, здесь hн = 100 см – ширина сечения нижней части колонны, lp – длина раскоса решётки,
По теореме Пифогора:
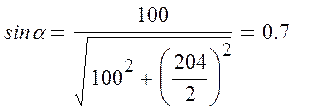
следовательно, α = 45º.
Для подбора сечения раскоса предварительно задаются гибкостью раскоса λр = 100. (можно от 100 до 120).
По (1, прил.7) в зависимости от гибкости λр = 100 определяется коэффициент продольного изгиба φ = 0.5634.
Требуемая площадь поперечного сечения раскоса определяется по формуле:
По сортаменту подбирается профиль раскоса в зависимости от Ар.тр.
Это равнополочный уголок с размерами полки 50 мм и толщиной полки 5 мм
Выписываются характеристики этого профиля:
- площадь поперечного сечения: Ар = 4.8 см²;
- минимальный радиус инерции из ix и iy, imin = 0.98 см.
Определяется гибкость стержня:
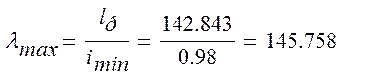
В зависимости от λmax = 145.758 по (1, прил.7) интерполяцией определяется коэффициент продольного изгиба φ:
При R
= 200 МПа:
При R = 240 МПа:
При R = 225МПа:
Определяется напряжение в раскосе:
4.6 Проверка устойчивости колонны в плоскости действия момента как единого стержня
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.