Matlab. Вычисления по заданной формуле при заданных значениях параметров

Санкт-Петербургский Государственный Политехнический Университет

Факультет технической кибернетики

Кафедра Автоматики и Вычислительной техники

Отчет

По расчетному заданию №0

Тема: MATLAB

Выполнил: студент гр.2081/3 

Проверил:

Санкт-Петербург

2009 г.

Задание №1.1

Вычислите указанное арифметическое выражение. Укажите последовательность нажатия клавиш. Сравните полученный результат с приведенным ответом.

>> x=(0.134+0.05)/(18+1/6-1-11/14-2/15*(2+6/7))

x =

    0.0115

>> y=0.0115;

>> if (x==y)

disp('true')

else

disp('false')

end

true

Задание №1.2

Проведите вычисления по заданной формуле при заданных значениях параметров. Укажите необходимую последовательность действий. Сравните полученный результат с приведенным ответом.

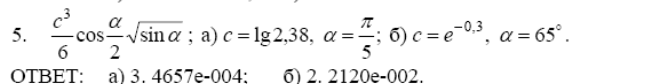
а)

>> format short e

>> c=log10(2.38);

>> l=pi/5;

>> x=(c^3)/6*cos(l/2)*sqrt(sin(l))

x =

  6.4897e-003

>> y=3.4657e-004;

>> if (x==y)

disp('true')

else

disp('false')

end

false

б)

>> c=exp(-0.3);

>> l=65/180*pi;

>> x=(c^3)/6*cos(l/2)*sqrt(sin(l))

x =

  5.4406e-002

>> y=2.2120e-002;

>> if (x==y)

disp('true')

else

disp('false')

end

false

Вывод: Полученные значения не совпали с предоставленными.

Задание №1.3

Выполните такие действия :

а) число z1, заданное в алгебраической (экспоненциальной) форме, переведите в экспоненциальную (алгебраическую), проверьте и запишите результат;

б) число z2, заданное в экспоненциальной (алгебраической) форме, переведите в алгебраическую (экспоненциальную), проверьте и запишите результат;

в) вычислите заданное выражение; запишите результат экспоненциальной

форме, причем аргумент результата обеспечьте в границах между (-π) и +π.

>> format long g

>> a=2.71*exp(i*pi)

a =

    -2.71 + 3.31879282568933e-016i

>> real(a)

ans =

   -2.7100

>> imag(a)

ans =

  3.3188e-016

>> abs(a)

ans =

                      2.71

>> angle(a)

ans =

          3.14159265358979

>> format short e

>> b=-0.7+4i

b =

 -7.0000e-001 +4.0000e+000i

>> abs(b)

ans =

  4.0608e+000

>> imag(b)

ans =

     4

>> real(b)

ans =

 -7.0000e-001

>> angle(b)

ans =

  1.7440e+000

>> c=1.31*exp(-i*5*pi/12);

>> d=-8-3i;

>> result=a^(1/2)/b*c-d

result =

  8.0470e+000 +2.4710e+000i

>> format long g

>> result

result =

           8.04696611916982 +      2.47101839960244i

>> angle(result)

ans =

         0.297934492247777

>> abs(result)

ans =

          8.41781418506258

Ответ:  result= 8.41781418506258*(cos(0.297934492247777)+i*sin(0.297934492247777))

Вывод: Простейшие действия с комплексными числами - сложение, вычитание, умножение, деление и возведение в степень - осуществляются при помощи обычных арифметических знаков +, -, *, /, \ и ^ соответственно.

Задание №1.4

Найдите корни квадратного уравнения  при заданных значениях коэффициентов a, b и c.

>> format short g

>> y=roots([5.09 4.32 256])

y =

    -0.42436 +     7.0792i

    -0.42436 -     7.0792i

Вывод: Уравнение имеет два комплексно-сопряженных корня.

Задание №1.5

Вычислите значения функции f(x) на отрезке [a; b] с шагом h.

>> y=sqrt(1+4*x).*sin(pi*x)

y =

  Columns 1 through 6

      0.36563      0.65979      0.95837       1.2379        1.476       1.6527

  Columns 7 through 11

       1.7515       1.7602       1.6719       1.4851       1.2046

Вывод:  Для вычисления значений функции на конечном множестве точек