





Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра компьютерных систем и программных технологий
Отчет по лабораторной работе №8
(Учебная дисциплина «Теория автоматического управления»)
Исследование автоколебаний нелинейных САУ
Работу выполнил студент группы №4081/2
Работу принял преподаватель___________
Санкт-Петербург
2010
1. Цель работы.
Теоретическое и экспериментальное определение параметров автоколебаний в нелинейных САУ
2. Исследуемая система.
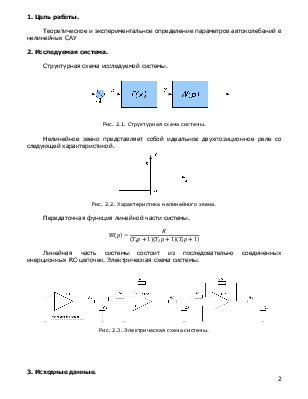
Структурная схема исследуемой системы.
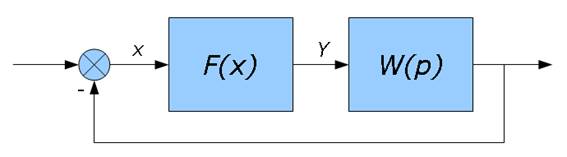
Рис. 2.1.
Структурная схема системы.
Нелинейное звено представляет собой идеальное двухпозиционное реле со следующей характеристикой.
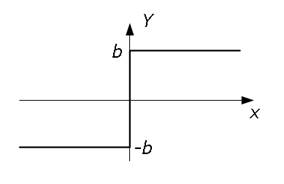
Рис. 2.2.
Характеристика нелинейного звена.
Передаточная функция линейной части системы.
![]()
Линейная часть системы состоит из последовательно соединенных инерционных RC-цепочек. Электрическая схема системы.
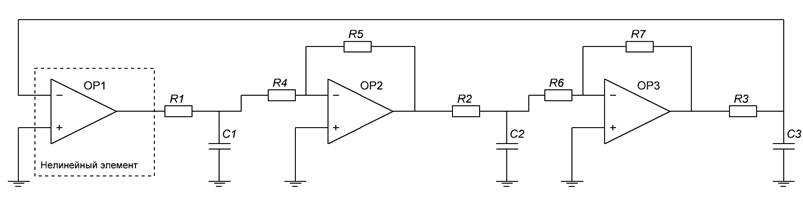
Рис. 2.3.
Электрическая схема системы.
3. Исходные данные.
Звено 1: R = 5 кОм, C = 0,5 мкФ,
T1 = 0.0025;
Звено 2: R = 2 кОм, C = 0,25 мкФ,
T2 = 0.0005;
Звено 3: R = 3 кОм, C = 1 мкФ,
T3 = 0.003;
Коэффициент усиления K изменяется при снятии характеристик, и задается как произведение коэффициентов усиления двух инвертирующих усилителей K1 и K2. Чтобы на снимаемые зависимости не влияло насыщение УПТ коэффициенты располагают, чтобы K1< K2. Звенья располагаются так, чтобы T1 > T2 > T3.
4. Гармоническая линеаризация.
Для исследования автоколебаний используется метод гармонической линеаризации. Он основан на предположении, что колебании на выходе нелинейного звена являются синусоидальными.
Разложим колебания на выходе нелинейного звена в ряд Фурье.
![]() ,
где
,
где
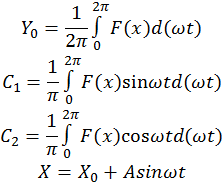
Рассматриваем только первую гармонику, так как предполагается, что линейна часть является фильтром нижних частот, иначе метод гармонической линеаризации не применим.
Запись уравнений в более удобной форме.
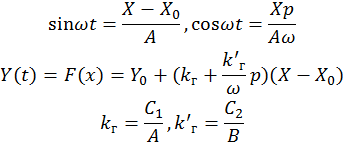
Нелинейная характеристика симметричная, входное воздействие равно 0, соответственно постоянную составляющую можно отбросить.
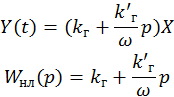
Расчет коэффициентов гармонической линеаризации.
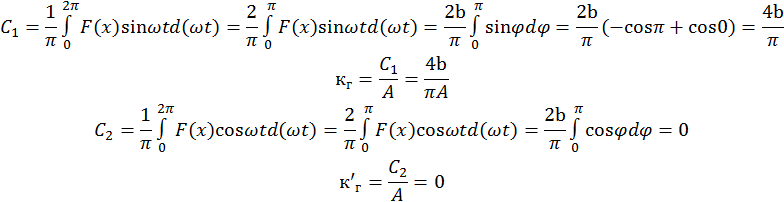
Эквивалентная линейная передаточная функция нелинейного звена.
![]()
Таким образом, передаточная функция эквивалентной линейной системы.
![]()
5. Расчет автоколебаний.
Необходимо рассчитать и построить зависимости:
• Амплитуды и частоты автоколебаний от коэффициента усиления линейной части системы;
• Амплитуды и частоты автоколебаний от постоянной времени второго звена при постоянном коэффициенте усиления линейной части системы.
Полученная передаточная функция эквивалентной линейной системы зависит от значения амплитуды и частоты выходного сигнала.
Амплитуду и частоту незатухающих автоколебаний можно найти рассмотрев систему на границе устойчивости. Это можно сделать с помощью известных критериев устойчивости.
По критерию Найквиста, система находится на границе устойчивости, если
![]()
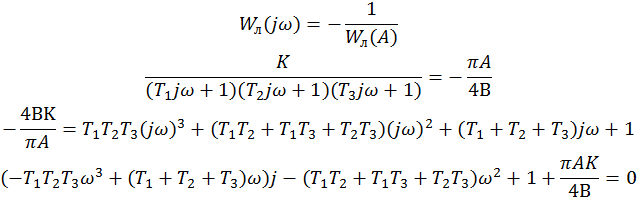
У полученного уравнения рассмотрим на равенство нулю отдельно мнимую и действительную части.
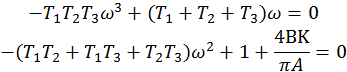
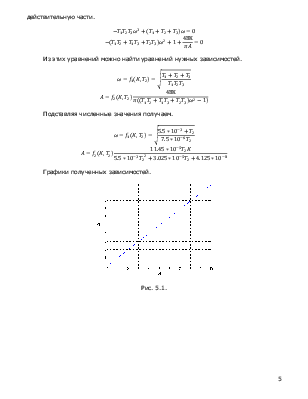
Из этих уравнений можно найти уравнений нужных зависимостей.
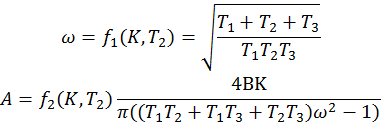
Подставляя численные значения получаем.
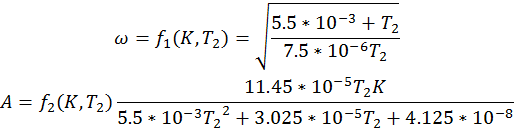
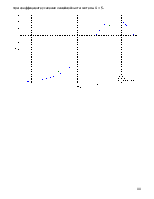
Графики полученных зависимостей.
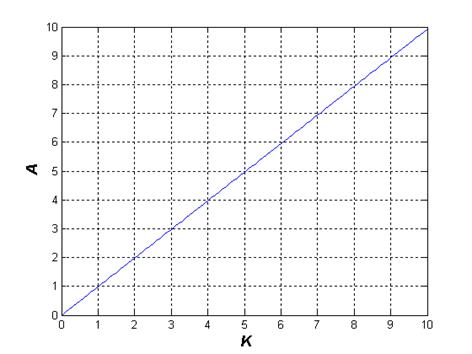 |
Рис. 5.1.
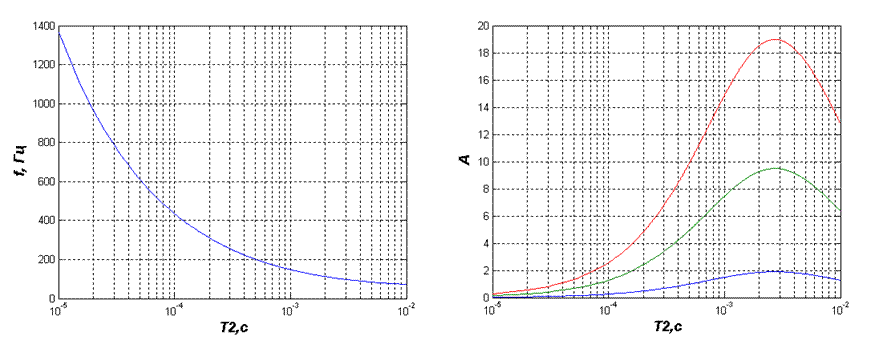 |
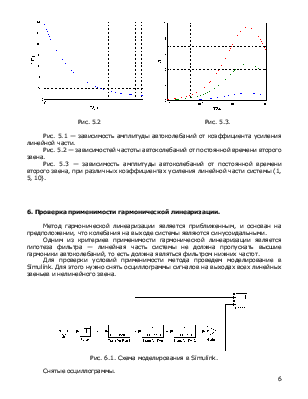
Рис. 5.2 Рис. 5.3.
Рис. 5.1 — зависимость амплитуды автоколебаний от коэффициента усиления линейной части.
Рис. 5.2 — зависимостей частоты автоколебаний от постоянной времени второго звена.
Рис. 5.3 — зависимость амплитуды автоколебаний от постоянной времени второго звена, при различных коэффициентах усиления линейной части системы (1, 5, 10).
6. Проверка применимости гармонической линеаризации.
Метод гармонической линеаризации является приближенным, и основан на предположении, что колебания на выходе системы являются синусоидальными.
Одним из критериев применимости гармонической линеаризации является гипотеза фильтра — линейная часть системы не должна пропускать высшие гармоники автоколебаний, то есть должна являться фильтром нижних частот.
Для проверки условий применимости метода проведем моделирование в Simulink. Для этого нужно снять осциллограммы сигналов на выходах всех линейных звеньев и нелинейного звена.
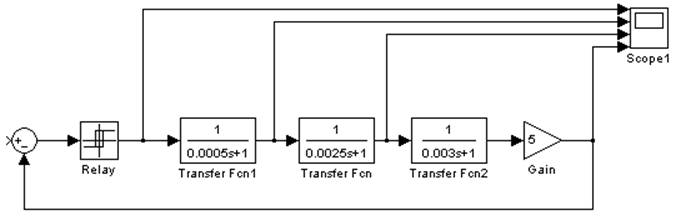
Рис. 6.1. Схема моделирования в Simulink.
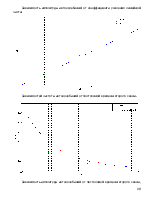
Снятые осциллограммы.
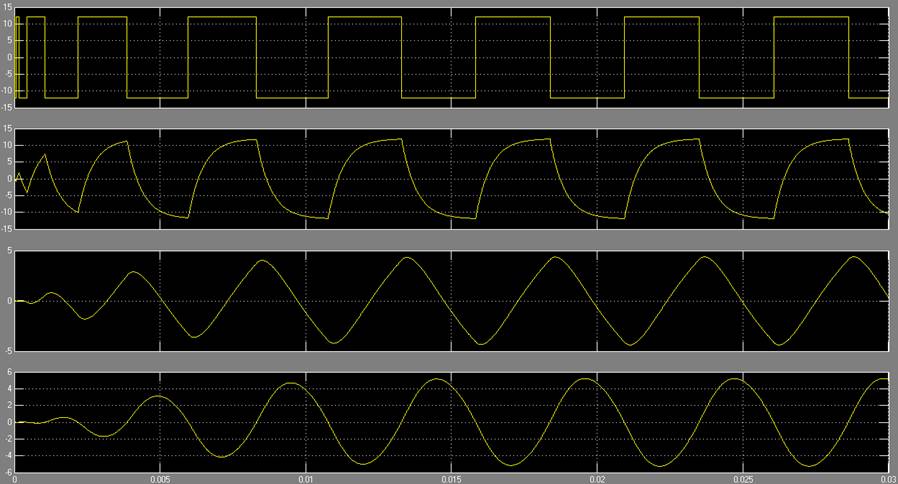
Рис. 6.2. Осциллограммы полученные в Simulink.
На основании полученных осциллограмм можно сделать вывод
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.